Understanding the Conditions for a Box to Topple Over
Written on
Chapter 1: Introduction to the Mechanics of Toppling
In this discussion, we will analyze the mechanics involved in determining the angle at which a box begins to topple. We consider a box that stands 2 meters tall and 1 meter wide, aiming to identify the minimum angle (illustrated in orange) of the ground necessary for the box to lose its stability. It is critical to note that we assume the ground possesses significant friction; otherwise, the box would simply slide down the incline without toppling.
To solve this problem, we must consider the center of mass of the box. Given its rectangular shape, the center of mass is located at its midpoint. The gravitational force acting on the box operates vertically downward from this center of mass. We can evaluate two scenarios to determine the conditions under which the box either remains stable or begins to topple.
An indented block of text can be used for citations or detailed explanations.
Section 1.1: Analyzing the First Case
In the first scenario:
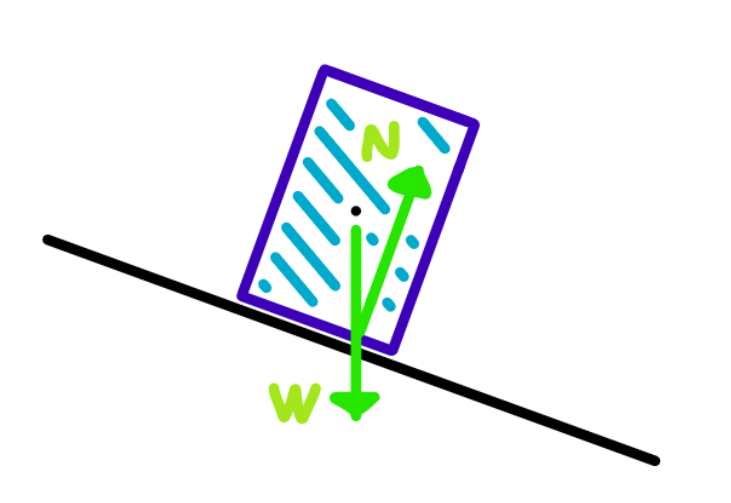
Image created by the author
The gravitational force W remains within the box's base, resulting in the equal and opposite reaction force N acting internally. Consequently, the box maintains its position without toppling.
Section 1.2: Exploring the Second Case
In the second scenario:
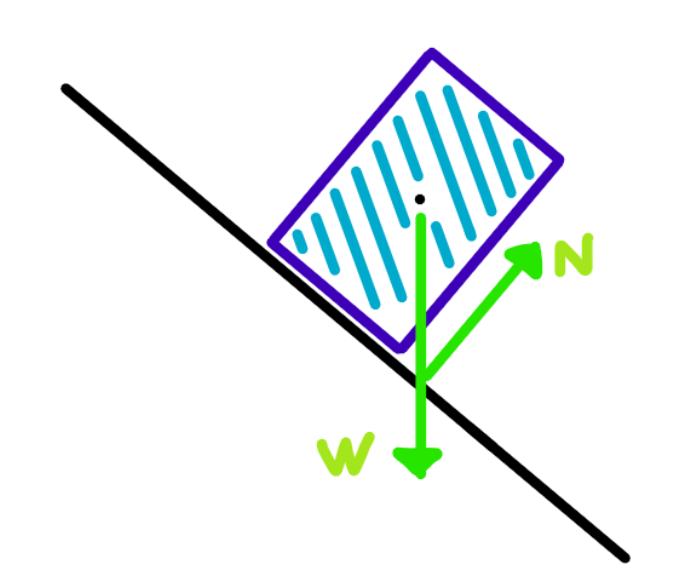
Image created by the author
Here, the gravitational force W extends outside the box's base, leading to the reaction force N acting externally. This configuration results in the box toppling over.
Chapter 2: Calculating the Critical Angle
To determine the precise angle at which the box topples, we must identify the angle where the reaction force aligns perfectly with the edge of the box. Given the box dimensions of 1 meter by 2 meters, we can illustrate this relationship.
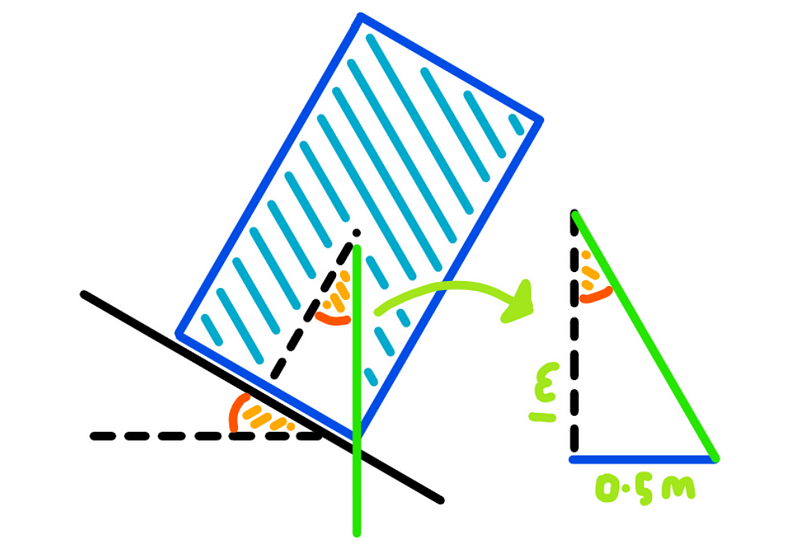
Image created by the author
By recognizing that the orange angles are equal, we can construct a triangle with two known side lengths derived from the box's dimensions, allowing us to calculate the desired angle. Let's denote this angle as ?.
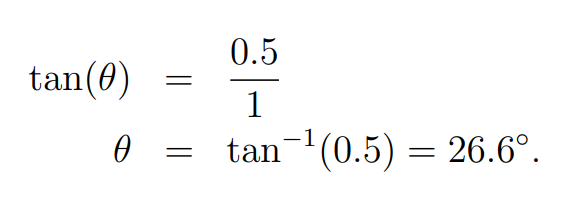
Image created by the author
Upon calculation, we find that for any angle exceeding 26.6°, the box will topple. This completes our analysis.
Extension: Considering a Square Box
While calculations provide clarity, you may also visualize the scenario conceptually. How would the toppling behavior change for a square box?
The first video, "At What Angle Will a Block Slide? Physics," explores the conditions under which a block will slide, providing valuable insights into this topic.
The second video, "Will a box TIP or SLIP if I push it? | Impending Motion of Rigid Planar Bodies | Doc Physics," delves into the impending motion of rigid bodies, further enhancing our understanding of toppling dynamics.