Counting Triangles: Unraveling Geometric Mysteries
Written on
Chapter 1: Introduction to Triangle Counting
Have you ever pondered how many triangles are present in a geometric figure? It’s not as straightforward as it might seem, especially when excluding additional elements like party decorations.

In various geometric designs, larger shapes can emerge from smaller ones. For instance, if you assemble four identical squares, you create a larger square that is four times the area of the individual squares. If I were to inquire about the total number of squares present, you would correctly conclude that it includes both the four small squares and the larger one, totaling five.
Today's challenge takes this concept further by focusing on a square made up of colorful triangles. A useful tip: consider the concept of rotational symmetry.
I encourage you to pause here, grab a pen and paper, and take a moment to engage with this challenge. Once you're prepared, continue reading for the solution!
Section 1.1: Understanding Rotational Symmetry
The solution revolves around a key concept: the square exhibits rotational symmetry with an order of four.

In the diagram above, observe the purple dot positioned at the top left of the square. Envision rotating the square 90 degrees clockwise. Each time the square rotates, its appearance remains unchanged if we ignore the purple dot.
This aspect is crucial, as every triangle—regardless of size—can be viewed from four different perspectives due to the square's rotational symmetry.
Section 1.2: Counting Triangles from Largest to Smallest
Our approach now is to start with the largest triangles and systematically work down to the smallest. The largest triangle consists of eight individual triangles.

Next, we have the second largest triangle, which comprises seven individual triangles.
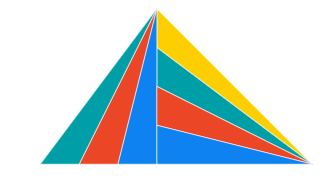
In general, we can identify four types of triangles that occupy more than a quarter of the square's area.

These triangles can be visualized in four different ways as the square is rotated 90 degrees four times. Therefore, we can calculate:
4 (4) = 16 triangles.
Now, let's consider smaller triangles. Can you employ a similar strategy to enumerate all the smaller triangles?
Let’s analyze a triangle formed by four of the smallest triangles.

This configuration yields four triangles, again due to rotational symmetry. Next, we can see two triangles made up of three smaller triangles, three triangles formed by two smaller triangles, and finally, four smallest triangles that stand alone.

This results in a total of 10 triangles! Multiplying this count by four gives us 40.
Thus, our grand total becomes:
16 + 40 = 56 triangles!
And that wraps up our exploration. (How many triangles do you see in the image below?)

How fascinating! What was your thought process during this exercise? Please share your insights in the comments; I’d love to hear from you!
Math Tricks and Tips
This first video demonstrates effective methods for counting triangles within geometric figures, offering tips and tricks to streamline the process.
The second video provides an easy approach to counting triangles, showcasing techniques that can help you solve similar problems in mere seconds!
Thank you for reading! If you found this article helpful, please consider sharing it with friends or expressing your appreciation through a clap.
