Chapter 1 Understanding the Sequence

Can you decipher the next number in this intriguing sequence?

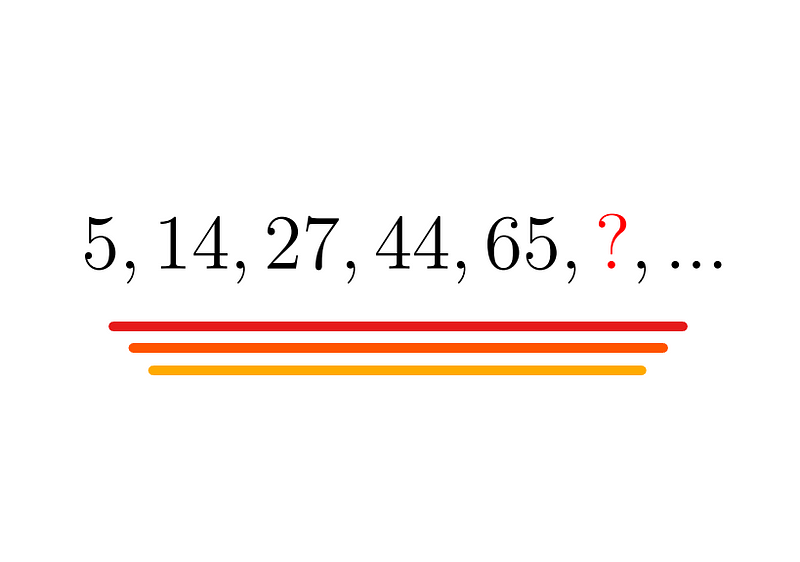
Once you've cracked the riddle, we will also look into how to predict any term in the sequence. Take a moment to think about it; the solution awaits below…

When the subsequent term isn’t clear from the visible pattern, we often analyze the intervals between the numbers.

The intervals are 9, 13, 17, and 21, showcasing a consistent increase of 4. Thus, the next interval will be calculated as 21 + 4 = 25. Therefore, the next term in the sequence will be 65 + 25 = 90, which solves the puzzle.

But let's go further! We can derive a general formula to find any term in this sequence. We will start by indexing the terms. Let's denote them as a, such that a(1) = 5, a(2) = 14, and so forth, with the last known a(6) being 90.

The differences are 9, 13, 17, 21, and 25, and the differences between those differences are consistently 4.

To understand this better, we consider the sequence of square numbers: 1, 4, 9, 16, and 25. The intervals between these numbers are 3, 5, 7, 9, and so on, with the differences between these intervals being constant at 2.

In this puzzle sequence, the second differences are twice that value (all equal to 4). Therefore, we conclude that our puzzle sequence can be expressed as a quadratic sequence multiplied by 2, or in simpler terms, a(n) = 2n² + ?.

Next, we need to determine the remaining component. By comparing a(n) to 2n²:

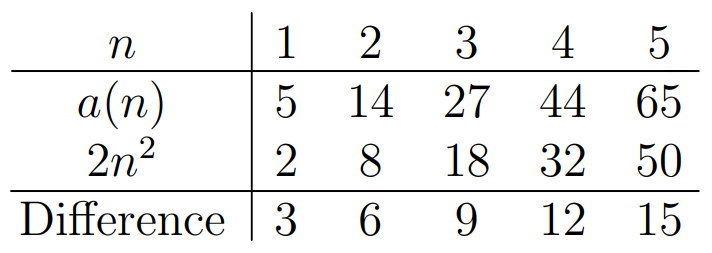
The differences between a(n) and 2n² yield a sequence made up of multiples of 3, which we can express as 3n.

Thus, we can formulate it as a(n) = 2n² + 3n.

Now, we can easily compute any term in the sequence. For instance, a(6) results in 72 + 18 = 90, which confirms our findings. Calculating further, a(100) equals 20300, and a(1000) equals 2003000.

Challenge: Earlier, we suggested that the second differences in a quadratic sequence remain constant. Why is this a valid assertion?

Chapter 2 Video Insights

The first video titled "Number Series Reasoning Tricks - The Easy Way!" provides a straightforward approach to unraveling number series puzzles.

In the second video, "Can you find the next number in this sequence? - Alex Gendler," the presenter challenges viewers to engage with mathematical sequences, further enhancing your understanding of the topic.