The Formula

The Abel Summation Formula is quite versatile. Here, I will present two specific instances that are particularly relevant, though they may not encompass its full generality. First, we need to clarify some notation. The notation [x] refers to the integral part of x (also called the integer part), indicating the largest integer less than or equal to x. Conversely, {x} denotes the fractional part of x, which can be expressed as x = [x] + {x}.

The Abel Summation Formula states that if f is a continuously differentiable function, then:

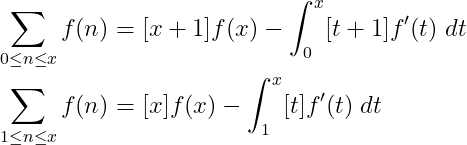
In essence, this allows us to convert a sum into an integral, which might be easier for us to calculate. It’s worth noting that the integral resembles a sum since the function [t] is piecewise constant.

Asymptotic Notation

Next, let's explore "Big O" notation, a brilliant way to express growth rates. The notation can be defined as follows:

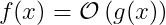
When we write this, it implies that there are constants K and c such that:

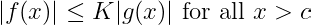
In simpler terms, this indicates that f is constrained by a multiple of g as the limit approaches infinity. Another perspective is that the ratio f/g becomes a bounded function in the limit.

The Harmonic Numbers

The harmonic numbers are defined by the following summation:

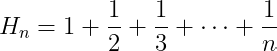
These numbers frequently appear in various mathematical contexts, particularly in number theory. Our goal is to estimate how these numbers grow. We apply the Abel Summation Formula to the harmonic numbers with f(n) = 1/n.

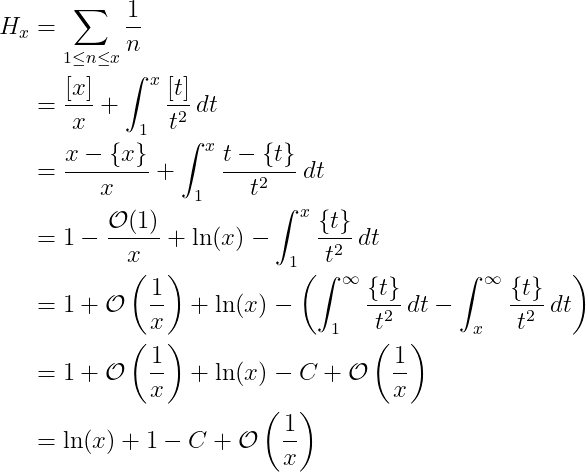
The constant 1 - C is often referred to as the Euler-Mascheroni constant, denoted as γ. The result we derive is:

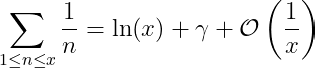
Notably, since 1/x approaches 0 as x approaches infinity, we conclude:

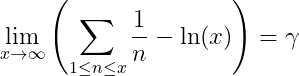
The constant γ appears in numerous analytical contexts and holds significant importance. Despite its prominence, its nature remains largely mysterious; it is unknown whether it is rational or irrational. However, we can compute its value to many decimal places, yielding approximately 0.5772156649.

Triangular Numbers

The ancient Greeks were aware of triangular numbers, which they viewed geometrically. They found these numbers particularly appealing, as they could be represented as triangular shapes. The initial triangular numbers are:

1, 3, 6, 10, 15, 21, 28, …

These numbers are obtained by summing the first n natural numbers, represented as follows:

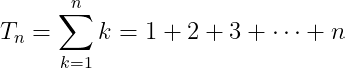
The term "triangular numbers" stems from the visual interpretation of these sums as forming a triangle, where the various terms correspond to layers within the triangle, illustrated below:

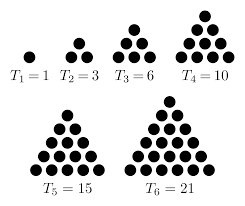
Finding a formula that generates triangular numbers typically involves guessing a polynomial expression and proving its validity through induction. However, we will take a different route, utilizing the Abel Summation Formula. Here, we consider f(n) = n, assuming n is an integer:

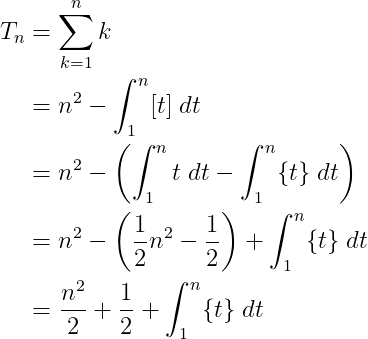
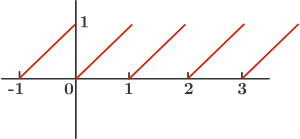
At this stage, it may seem that we are faced with a complex integral. However, it simplifies significantly since {t} is a periodic function that forms a triangle with an area equal to half the unit square's area across all whole number intervals on the real line.

Thus, we derive:

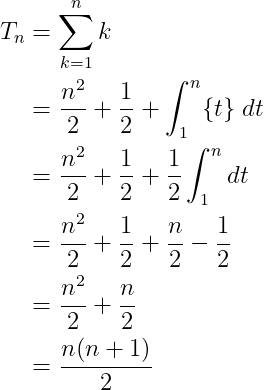
We have successfully demonstrated that:

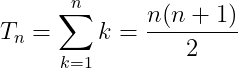
Feel free to verify this by calculating the values yourself!

The Riemann Zeta Function

Let's consider the partial sums of the well-known series for the Riemann zeta function. By applying the Abel Summation, we arrive at a fascinating outcome:

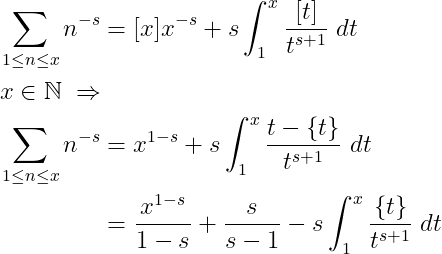
Assuming Re(s) > 1 allows us to take the limit as x approaches infinity on both sides, yielding:

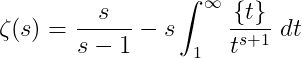
This result is remarkable. It clarifies the origin of the pole of the zeta function at s=1 and provides an analytic continuation of "the zeta function defined as a series," as the right-hand side converges for Re(s) > 0. This opens up the possibility of analyzing the non-trivial zeros of the zeta function, which we know do not lie on the line s=0.

Abel Summation on Taylor Series

For our final example, I will demonstrate an intriguing representation of the natural exponential function. Before proceeding, we must introduce two essential functions: the gamma function Γ(z) and the digamma function ψ(z). The gamma function possesses the property Γ(z+1) = zΓ(z), making it a generalization of factorials. By induction, it can be shown that Γ(n) = (n-1)!. The digamma function is defined as the logarithmic derivative of the gamma function, satisfying ψ(z+1) = ψ(z) + 1/z. They are defined as follows:

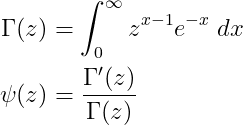
The gamma function can be extended to the entire complex plane, except at non-positive integers where it has poles. Recall the Taylor series for the exponential function:

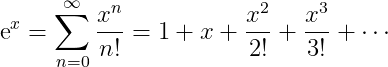
By manipulating this series and applying the Abel Summation, while being cautious to differentiate with respect to the running variable rather than x, we obtain:

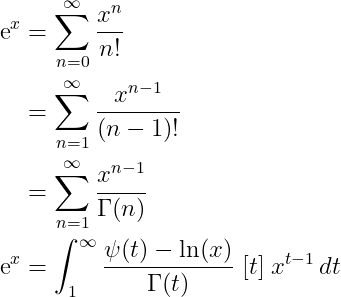
This result is intriguing! We can immediately verify the property of the exponential function regarding its invariance under differentiation. Let's check this:

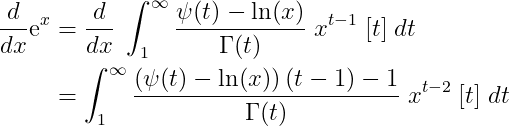
Next, we substitute within the integral and utilize the properties of our special functions:

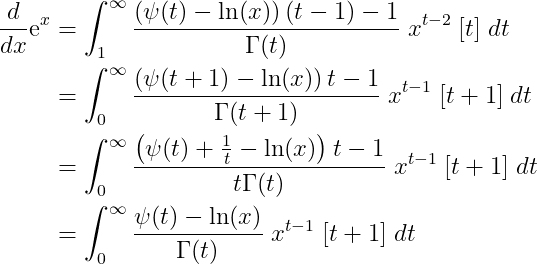
This corresponds to the series:

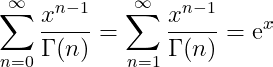
The transformation rules of Γ and ψ ensure that differentiation invariance holds. The equivalence of the series above requires further justification, as ψ is not defined at 0. Nevertheless, we observe that:

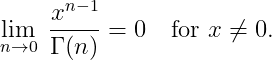
It's important to note that this integral expression for the exponential function is only valid for x > 0 due to the logarithm's constraints. Perhaps there is a way to extend it?

Outro

The Abel Summation Formula serves as a robust tool, having been employed to establish numerous fascinating theorems. There are undoubtedly many more theorems waiting to be uncovered with this formula's assistance. I have highlighted several series and sums that I find captivating, but I encourage you to discover your own sums and transform them into integrals to see what results you achieve.

Happy (Abel) summing!

The first video titled "10c - Abel's Partial Summation Formula" provides an insightful overview of the Abel Summation Formula, illustrating its significance and applications in mathematics.

In the second video, "Abel's Summation by Parts," viewers can explore the techniques and methodologies related to this powerful mathematical tool, enhancing their understanding of the subject.