Can You Determine the Probability?

In this exciting problem from the Oxford MAT of 2003, we delve into a playful game involving a fair die. Why not grab a friend or a loved one and see who can roll a six first? The objective is to calculate the likelihood that the first player, who rolls the die initially, will be the first to achieve a six.

Hint: You might notice a geometric sum emerging during your calculations!

Take a moment to pause here, grab a pen and paper, and give it a shot before continuing for the solution! 🎲

Solution Overview

The game unfolds as follows: Player 1 rolls first. If they roll a six, they win, and the game concludes. If not, Player 2 takes their turn.

The essential point to note is that for Player 1 to win on any given roll, Player 2 must have previously failed to roll a six.

The probability of Player 1 rolling a six on their first attempt is straightforward: it's 1/6.

Next, if Player 1 does not roll a six (with a probability of 5/6), Player 2 also has a 5/6 chance of not rolling a six on their turn. When Player 1 rolls again, they again face a 1/6 chance of success.

Consider another scenario where Player 1 tries again...

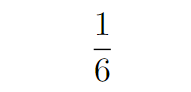
In the situation where Player 1 aims to win on their second attempt, both players must have failed to roll a six in their previous attempts. This scenario can be expressed as a product of four fractions, with the last fraction (1/6) representing the chance that Player 1 finally rolls a six on their second try.

Can you identify a pattern? What happens if Player 1 wins on their third, fourth, or even fifth attempt?

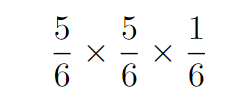
Take your time to think this through. The solution requires considering all the potential ways Player 1 can win, whether it’s on their first roll or their 2024th!

In general, if Player 1 wins on their nth roll, the total number of (5/6) fractions will equal 2(n-1). For instance, if Player 1 clinches victory on their sixth roll, then both players must have failed five times each, leading to a total of ten failures (2(6–1) = 10).

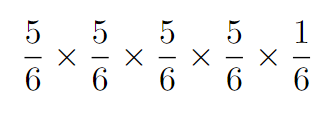
The infinite sum derived from this analysis reveals the overall probability of Player 1 winning.

Geometric Sum to Infinity

To find the total value of our sum, we can apply the formula S = a/(1-r), where 'a' is the initial term and 'r' is the common ratio.

And there you have it—the final answer! Isn’t it fascinating?

What insights did you gain from this exercise? Feel free to share your thoughts in the comments below; I’m eager to hear your perspectives! 😊

Math Puzzles

If you're interested in more engaging math puzzles, check out the best math puzzles available on Medium. Explore various topics like Algebra, Geometry, Calculus, and Number Theory!

The first video provides an example of finding probability, showcasing techniques in Probability and Statistics.

The second video focuses on calculating the probability of an event, offering further insights into this fascinating subject.

Thank you for taking the time to read through this! If you found the content helpful, don’t hesitate to show your appreciation by clapping for the article.

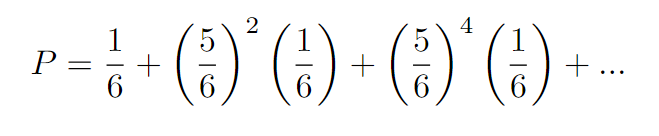
Are you ready to challenge someone to this dice-throwing game? Your support means a lot to me, so if you're feeling generous, consider buying me a coffee to help sustain my writing journey!

With gratitude, Bella ❤️