Chapter 1: A New Perspective on Derivatives

If you've ever enrolled in an introductory calculus course, you likely encountered a set of derivative rules that you were expected to memorize. In this discussion, I aim to introduce a more straightforward method for applying the product and quotient rules. Let's begin with the product rule.

Historically, Gottfried Leibniz, one of the co-founders of calculus, is credited with formulating the product rule. He originally expressed this rule using differentials, but for clarity, I will utilize prime notation, which was introduced by Joseph Lagrange.

Standard Product Rule

The traditional formulation of the product rule is effective, yet there is room for refinement. Here’s a brief proof for those who may not be familiar with it. (If you already know the proof, feel free to skip this section.)

To evaluate the limit, we must be inventive and add zero in a strategic way.

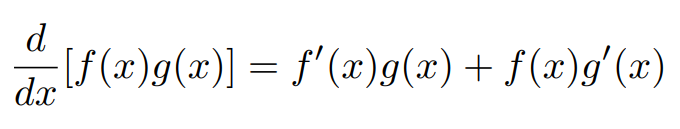
We can separate this limit into two manageable components.

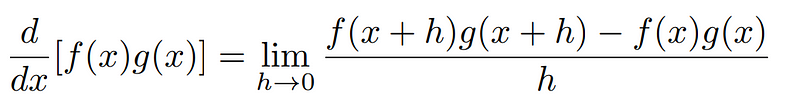
Next, we apply the product rule of limits to simplify the expression.

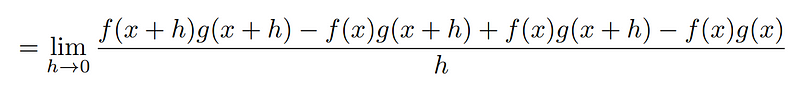
At this point, we can extract f(x) from the second limit because it remains constant with respect to h, the variable approaching zero.

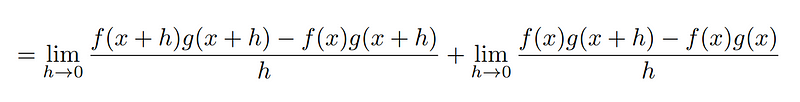
This process leads us to the conventional product rule commonly found on formula charts.

A Simplified Variant

What if we divided the original function by its derivative? We arrive at—

By simplifying, we ultimately get—

Modified Product Rule

What insight does this provide? I believe it allows us to break down a derivative into two fundamental components: the magnitude and the "unit" change.

The magnitude functions as a scaling factor for the "unit" change, aligning it with the derivative's value at a specific x.

The "unit" change can be viewed as a summation of ratios. I refer to it as "unit" change because the rate of change of each function is adjusted by the magnitude of the original function.

Benefit #1: Versatility

One significant advantage of this formula is its flexibility. Let’s use it to derive the quotient rule starting with y = f(x)/g(x). The derivative yields:

Expressing a Quotient as a Product

By applying the new formula, we have:

This expression is somewhat complex, so let’s break it down. First, we can simplify the derivative of 1/g(x) using the chain rule:

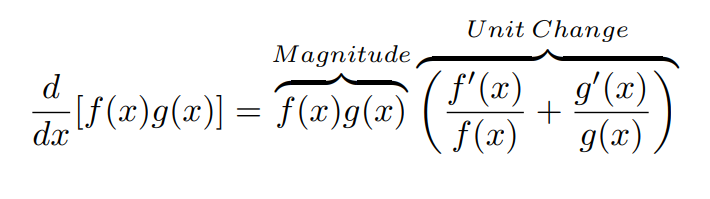
Substituting this simplified derivative back into our original formula yields:

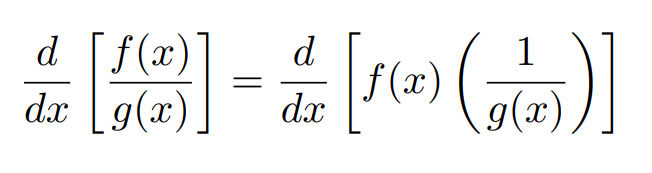
This can be further simplified to:

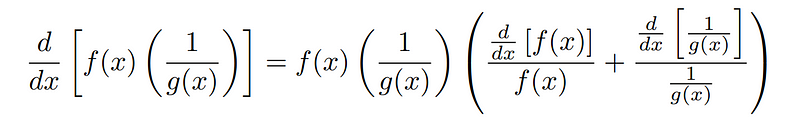
Modified Quotient Rule

I find this variation of the quotient rule particularly useful as it resembles the product rule, with the sign reversed for the term g’(x)/g(x) because g(x) appears in the denominator. This aligns with the intuitive idea that if g(x) grows faster compared to f(x), the overall derivative should decrease.

Benefit #2: Expandability

Another advantage of this formula is its ease of expansion when dealing with multiple functions. Let’s see how this unfolds.

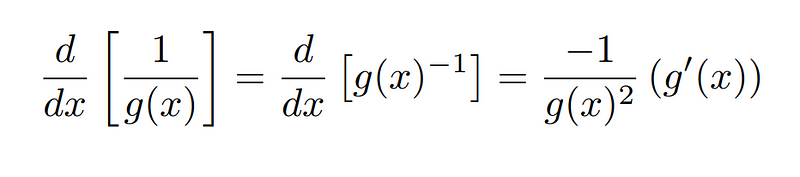
Similarly, for the quotient rule:

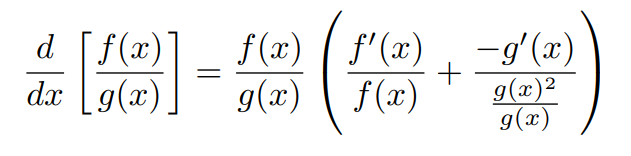
Drawback: Continuity and Differentiability

While combining the first two benefits can simplify complex problems, it does come with certain limitations. For instance, consider the derivative of x³sin(x)/2.

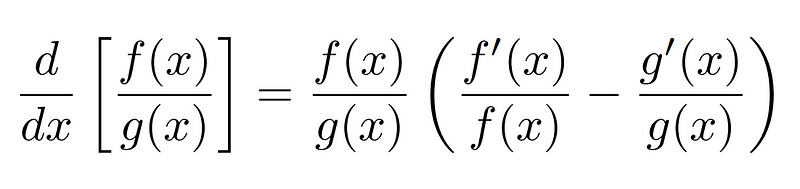
The expression might be factored, but it does not equate to the actual derivative. This occurs because the current dy/dx is undefined at points where x = 0, π, 2π, etc. The reason is that we are dividing by x³ and sin(x), making dy/dx undefined at x=0 or when sin(x)=0.

To address this issue, we could multiply the expression within the parentheses by a factor of x*sin(x), allowing us to evaluate dy/dx at x=0, π, 2π, etc. Thus, our concluding result is—

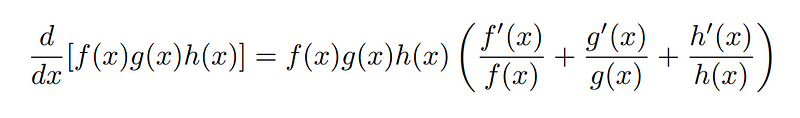
Now, let’s explore the derivative of y = tan(x)/(√x³).

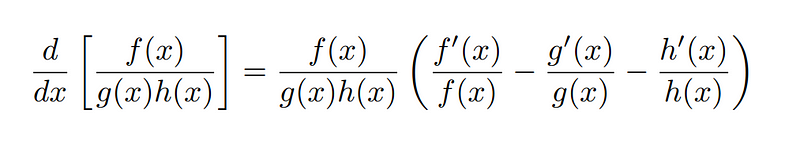
To determine if we need to expand this expression, we must ascertain the domain of the original function. Since √(x³) is in the denominator, we know that x must be greater than 0. Additionally, tan(x) is undefined when cos(x) = 0, so the function y is defined when x > 0 and x ≠ π/2, 3π/2, etc.

These domain restrictions also apply to dy/dx, but dy/dx introduces an additional sin(x) in the denominator, creating further restrictions. Therefore, we need to include tan(x) in the parentheses to ensure dy/dx can be computed for all permissible x-values.

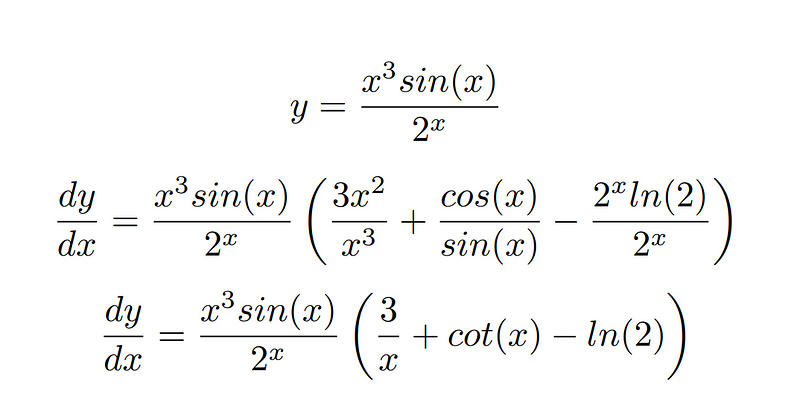
The critical takeaways from this discussion should be the following three formulas:

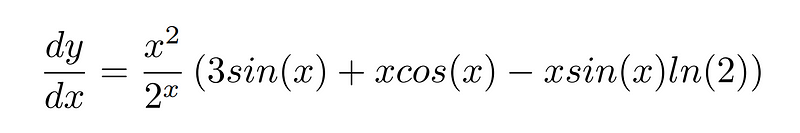
Conclusion

I find this approach intriguing as it provides a streamlined way to articulate derivatives that would typically be laborious to express. Moreover, I believe this formula should become the standard due to its memorability and intuitive nature.

Thank you for taking the time to engage with this article. If you enjoyed this content, consider subscribing for more insights. Until next time!

Chapter 2: Enhancing Understanding with Video Resources

Explore essential derivative tricks that are often overlooked in traditional calculus courses. This video will help you master concepts quickly and effectively.

Dive into a comprehensive beginner's guide on derivatives that simplifies complex ideas and provides a solid foundation for your calculus studies.