Introduction

Recently, I came across an intriguing puzzle presented by Hemanth in his excellent publication, Street Science. The challenge involves a grocer who seeks to acquire a set of weights that will allow him to balance items weighing up to 40 kilograms (kg), all while minimizing the number of distinct weights he needs.

To clarify, the grocer aims to obtain weights that are whole numbers in kilograms, specifically the least number of weights necessary to balance objects up to 40 kg. The objective is to determine the specific weights required and their total count.

For visualization, consider the type of weighing scale depicted below:

Photo by Elena Mozhvilo on Unsplash

For instance, if the grocer possesses weights of 3 kg and 5 kg, placing both on one side allows for the measurement of an object weighing 8 kg on the opposite side. Importantly, as Hemanth points out, weights can be placed on either side of the scale. Thus, with weights of 3 kg and 5 kg, it’s possible to measure an object that weighs 2 kg by placing the 3 kg weight on the same side as the object.

Hemanth proposes a compelling solution to the puzzle: the minimum number of weights required is four: 1 kg, 3 kg, 9 kg, and 27 kg. These weights are notable as they represent powers of 3. This is significant because each weight can occupy one of three positions: on the left side, on the right side, or not used at all. The total combinations available with four weights is therefore 3^4 = 81. However, this total includes negative outcomes; for instance, if a 3 kg weight is placed on the right with the object, and nothing on the left, the scale can only balance if the object weighs -3 kg. Since we seek only positive outcomes, the number of valid combinations is (81 - 1) / 2 = 40, where the -1 accounts for the exclusion of 0 from our results to maintain balance between positive and negative outcomes.

To further explore this concept, I decided to verify that Hemanth's strategy holds true for all weights, not just those up to 40 kg, through mathematical induction. If you're unfamiliar with this technique, you might want to check out the Wikipedia page for a deeper understanding.

Mathematical Induction Proof

We aim to establish the following assertion P(m) is valid for every integer m > 0:

P(m): The integer m can be represented as the sum of the first k powers of 3, each multiplied by -1, 0, or 1.

Inductive Step

This step is slightly more complex but manageable. We need to demonstrate that if P(n) holds for some integer n, then P(n + 1) must also be valid.

Assuming P(n): we can express n as the sum of the first k powers of 3, each multiplied by -1, 0, or 1. We can represent n mathematically as follows:

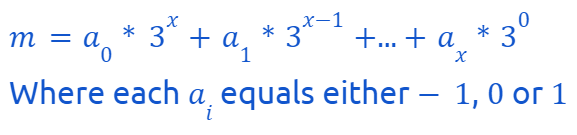
Our goal is to prove that we can express n + 1 in a similar manner. Essentially, we need to demonstrate that by modifying one of the a variables, we can increase the total sum by 1.

Indeed, this is possible! By transitioning from

we can increase the first a variable that is less than 1 by 1 while changing all a variables with a higher index to -1. The justification for this change can also be proven through mathematical induction. It’s important to note that changing an a variable from 1 to -1 effectively subtracts the corresponding power of 3 twice, while increasing an a variable that is less than 1 adds the corresponding power of 3 once. Therefore, we aim to prove the following statement:

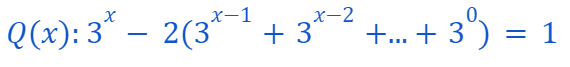
For every integer x > 0. This is because we assert that adding

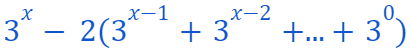
to any integer n will yield n + 1.

Base Case Confirmation

Our base case asserts that

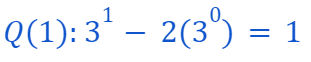
This can be easily demonstrated since

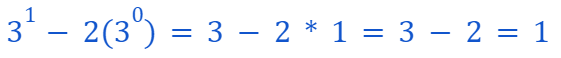
Thus, our base case is validated.

Inductive Step Confirmation

Given

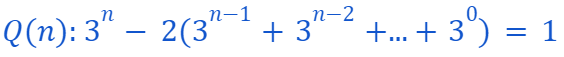
we need to show

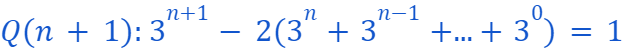
This leads us to:

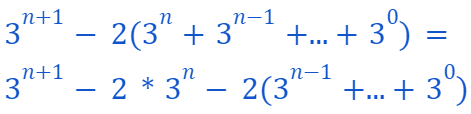
Note that

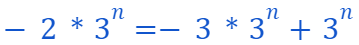
Thus,

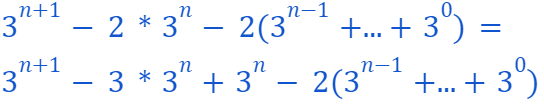
As a result, we can conclude that

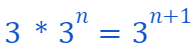
Hence, we have established that

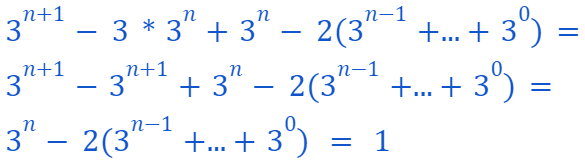
This last assertion is validated by the inductive step assumption! Consequently, we have successfully demonstrated that

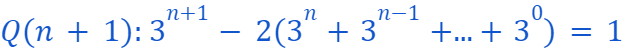
is derived from

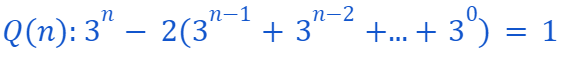
This confirms that our overarching inductive step is complete, leading to the proof that:

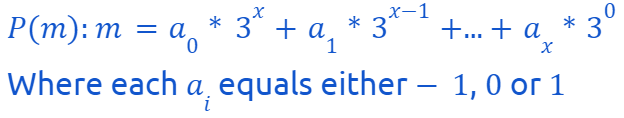
holds true for every integer m > 0.

Q.E.D. Thank you for reading, and special thanks to Hemanth for presenting such an engaging puzzle!

Video Explanation

In order to fully grasp the intricacies of this puzzle, you might find the following resources helpful:

The first video titled Can you solve the classic 12 marbles riddle? (Detailed Solution Video) provides a comprehensive breakdown of similar mathematical challenges.

Additionally, the second video, Pan balance with a "double scales" - puzzle problems for 4th grade and up, offers engaging puzzle scenarios suitable for a younger audience while still being thought-provoking.