Chapter 1 Understanding Supplementary Angles

When two angles combine to form a straight line, their total is always 180°. This fundamental fact, while common knowledge, is just the beginning of a deeper exploration. Supplementary angles possess intriguing characteristics that are essential in trigonometry. They can be particularly useful when proving the law of sines for obtuse triangles, making them a vital concept to grasp. So, what exactly do we need to uncover? Let’s delve into it.

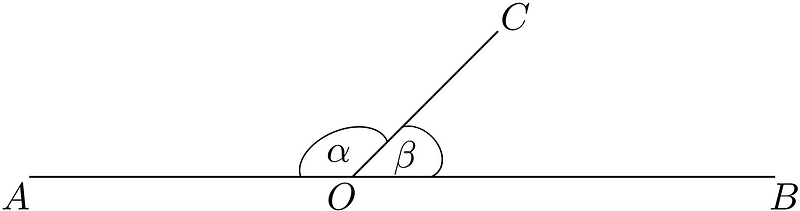
To start, consider a straight angle divided into two parts, which we can label as θ and 180° - θ:

These two angles together must equal 180°, represented as:

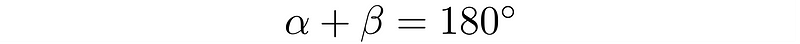
It’s important to note that knowing one angle allows you to easily determine the other.

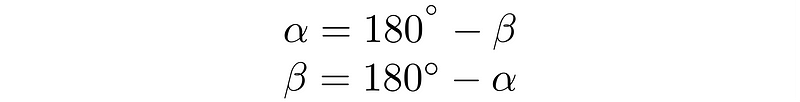
Remember, θ and (180° - θ) don’t need to be adjacent on a straight line. The following discussions apply to any two angles that sum to 180°, regardless of their positioning, even if they are in separate figures or situations.

The Sine Identity

As a straight angle equals 180°, both θ and (180° - θ) fall within the interval of (0, 180°). Let's select a point for θ on our diagram, for example:

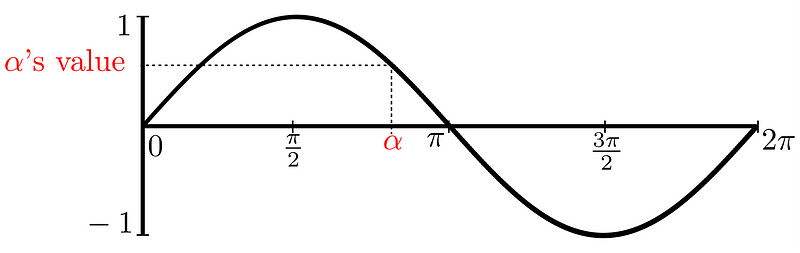
Now, what is the value of (180° - θ)? We know that (180° - θ) = θ. Because of the sine function’s symmetry, the sine of θ will equal the sine of (180° - θ). Take a look at the following illustration:

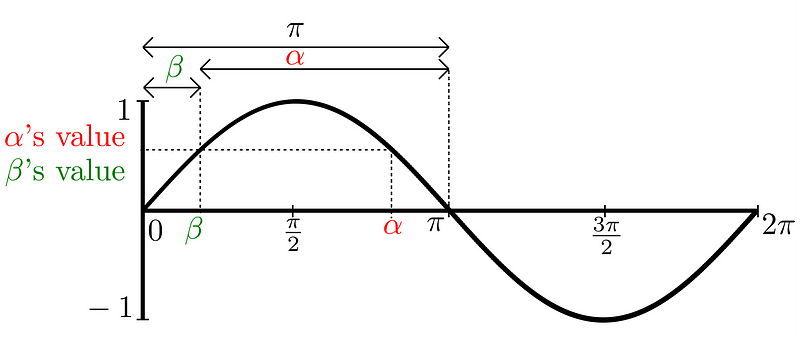
Thus, we can conclude:

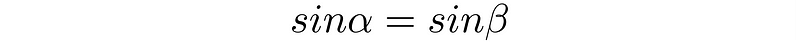
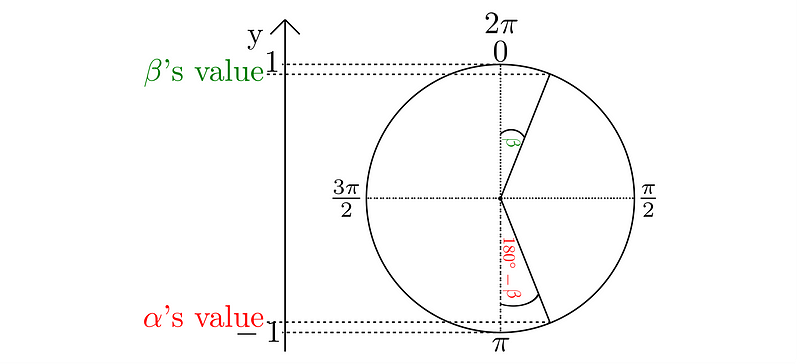
This identity can also be represented using a unit circle, as shown below:

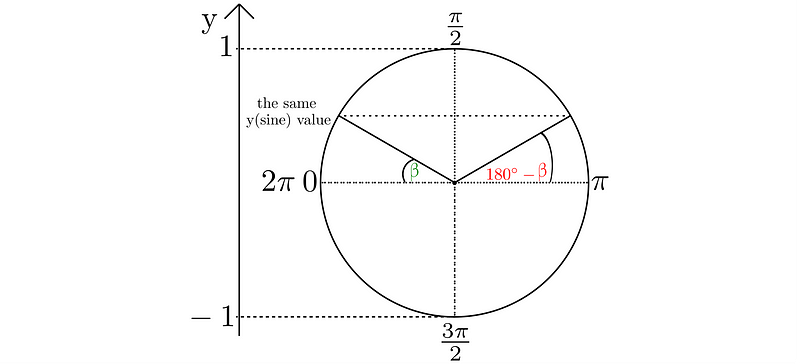
The Cosine Identity

Now, shifting our focus to cosine, we see that the angles remain within the interval of (0, 180°) since we are still dealing with the same straight angle of 180°. The cosine values vary from 1 to -1 within this range. The question now is: what relationship exists between our two angles? Let's again choose a point for θ on the graph.

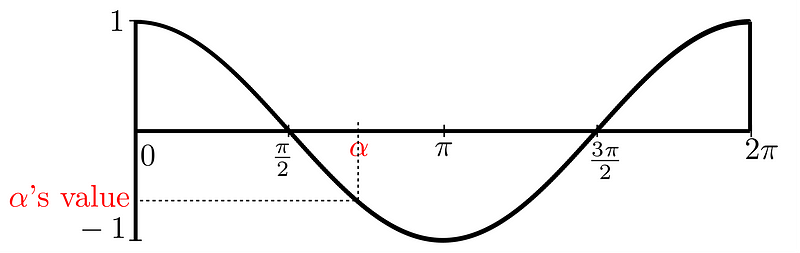
Now, we can calculate the value of (180° - θ).

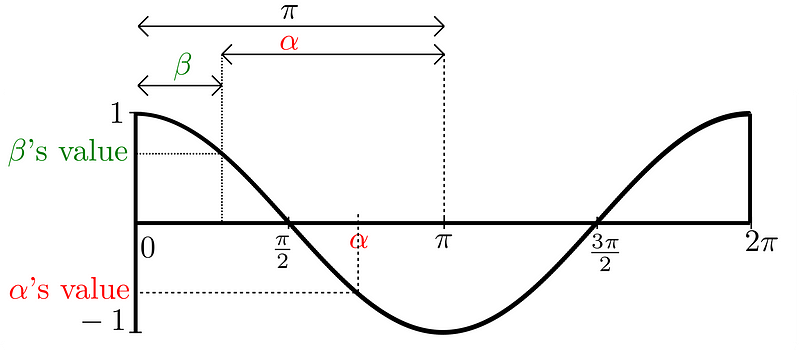
Since adding θ to (180° - θ) results in 180°, and due to the symmetry of the cosine function, the cosine values for these two angles must be opposites. Thus, we can express:

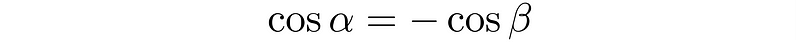
Similar to the sine identity, this can also be illustrated on a unit circle with the radians appropriately set for the cosine function.