Setting the Stage

Before diving in, ensure you're in light mode to view the equations clearly. We will introduce a new symbol, denoted as ε, often referred to as the dual unit. This unique number has the defining property that ε² = 0 and ε ≠ 0. A dual number takes the form a + bε, where a and b are real numbers, known as the real part and dual part, respectively.

The usual arithmetic rules apply here, except division by a number of the form bε is not permitted, which will be significant later. Although this number system may seem trivial at first glance, it conceals some fascinating secrets that I am eager to unveil.

By observing that multiplying by the dual conjugate, i.e., (a + bε)(a - bε) = a², yields a different norm than those typically encountered in complex analysis, we can explore further. Additionally, expanding functions into their corresponding power series (essentially representing them as infinite-degree polynomials) enables us to evaluate well-known functions using dual numbers.

For instance, the exponential function can be expressed as follows:

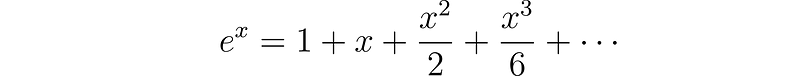
Consequently, we find that

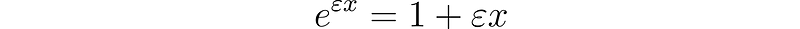
This results in several important equations, which may initially appear incorrect, yet are indeed valid.

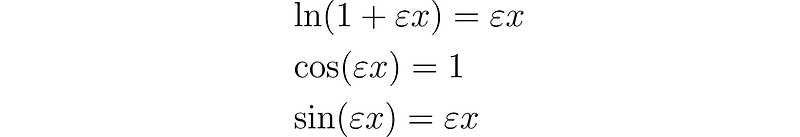
It may take some time to adjust to working within the realm of dual numbers!

Algebraic Derivatives with Dual Numbers

The dual numbers prove particularly useful when analyzing functions. The following remarkable statement holds true:

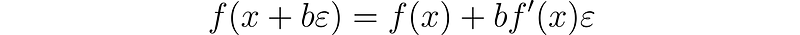
Here, x and b are real numbers. Notably, setting b = 1 results in a beautiful functional equation:

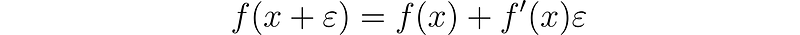
This equation will be fundamental to our analysis throughout the article. We will refer to the first as "the general dual functional equation" and the second as "the dual functional equation."

It's essential to note that this method is guaranteed to work only for analytic functions, though it applies to a much broader range. We will not delve deeply into this, but exercise caution when employing this technique.

Observe how closely this resembles the standard definition of the derivative, yet it intriguingly omits the limit. While it may be tempting to isolate f´(x) in this expression, remember that division by ε is not permitted, which introduces uncertainty.

However, this framework offers remarkable power, as we will soon demonstrate.

Let’s begin with a straightforward example: for f(x) = x², we evaluate f(x + ε) = (x + ε)² = x² + 2xε. Consequently, we know that the dual part represents the derivative, yielding the result of 2x.

Now, let's tackle a more complex function, such as f(x) = sin(x). Applying a trigonometric identity, we can write:

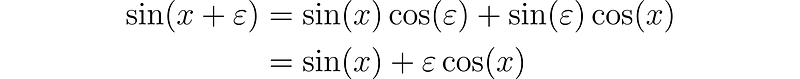
Thus, by the dual functional equation, we find that f´(x) = cos(x).

Now, let’s challenge ourselves with the square root of x, which is not differentiable at x = 0. We approach this with care:

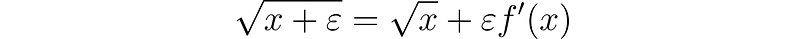
By squaring both sides and utilizing the property of the dual unit, we obtain:

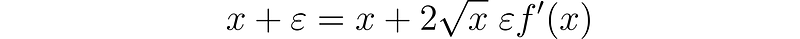
By comparing the dual parts, we reach the conclusion:

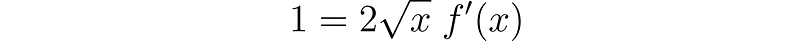
Which can be expressed in a more recognizable format:

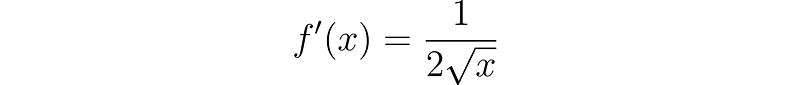
This is indeed accurate.

Now, let’s test this method further with a function that presents difficulties with sums, like the natural logarithm. Can we differentiate it using this approach?

Assuming we are unsure of the derivative of the natural logarithm, we denote it as DL(x) = d/dx ln(x). We can express this as:

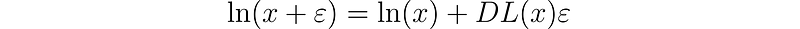
Taking the natural exponential function on both sides, we arrive at:

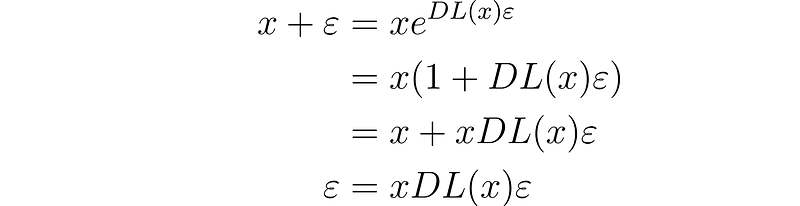
By comparing the dual parts on both sides, we conclude that x DL(x) = 1, which implies that DL(x) = 1/x, or in conventional notation, d/dx ln(x) = 1/x.

Now, let’s tackle a final challenge: finding the derivative of the function f(x) = x^x.

No problem!

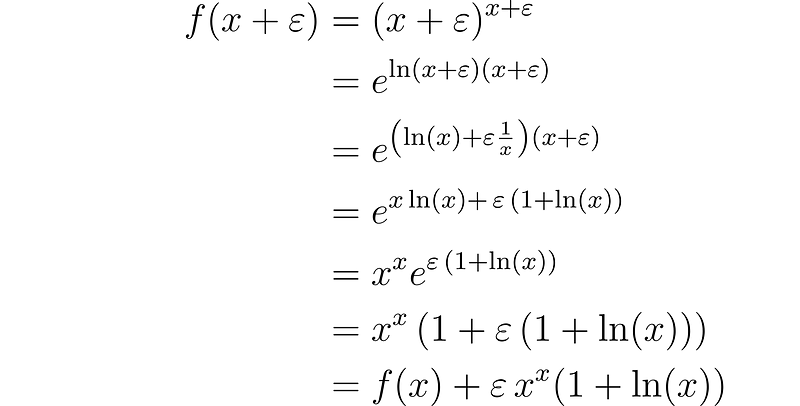
By applying several of our previously derived properties, we find that the derivative corresponds to the dual part of this expression:

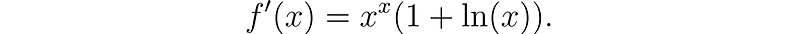
Isn’t that impressive?

We can continue utilizing this method to derive more derivatives, but its power extends beyond merely finding these derivatives for specific functions. Remarkably, we can also use it to "prove" all the fundamental rules of differentiation.

Proving Differentiation Rules without Limits

Let’s utilize this approach to validate the product rule:

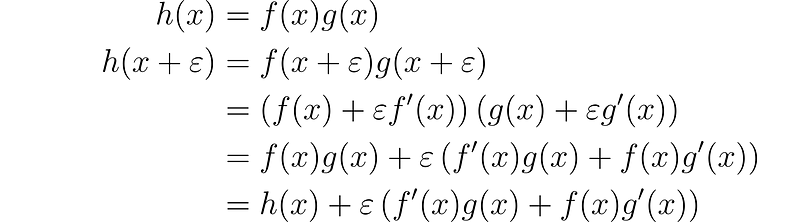
This immediately leads us to h´(x) = f´(x)g(x) + f(x)g´(x), which is a familiar result!

Next, let’s tackle the quotient rule.

Now, what about the chain rule? Let h(x) = f(g(x)). We can express this as:

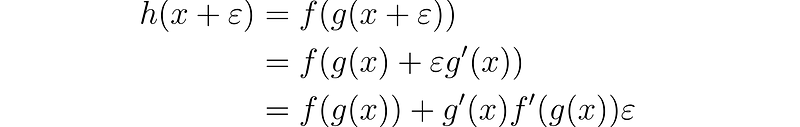
In doing so, we have employed the general dual functional equation with g´(x) acting as the constant b in the equation.

Did we just prove the chain rule in just three lines? Yes, we did!

The only mnemonic you need to excel at differentiation is ε!