The Optical Illusions of Spinning Wheels: A Deep Dive
Written on
Chapter 1: Understanding the Wagon Wheel Effect
In a recent Saturday evening, I stumbled upon a captivating advertisement while watching a YouTube video. The stunning visuals and smooth road were impressive, but what truly intrigued me was the car's wheels. Despite the vehicle moving forward, the wheels appeared to spin in reverse. This intriguing visual phenomenon is known as the wagon wheel effect. One might speculate that this is due to special rims or clever editing tricks. However, the explanation lies elsewhere—no special equipment or film tricks are needed. Variations of this effect can be found beyond spinning wheels; for instance, consider this video of a helicopter with seemingly static rotors.
This optical illusion can be understood through the concept of 'aliasing,' which plays a crucial role in digital signal processing. Although aliasing can manifest in various scenarios, using the example of a wheel effectively demonstrates how this phenomenon occurs across different fields.
Section 1.1: The Intuitive Approach to the Wagon Wheel Effect
Picture a wheel turning at a rate of one revolution per minute (1 rpm), while a camera captures images at a shutter speed of one frame per minute (1 fpm). In this case, the camera only records the wheel once it has completed a full rotation, leading to the illusion that the wheel is stationary. This situation was evident in the helicopter video, where the camera's shutter speed aligned perfectly with the rotor's rotation.
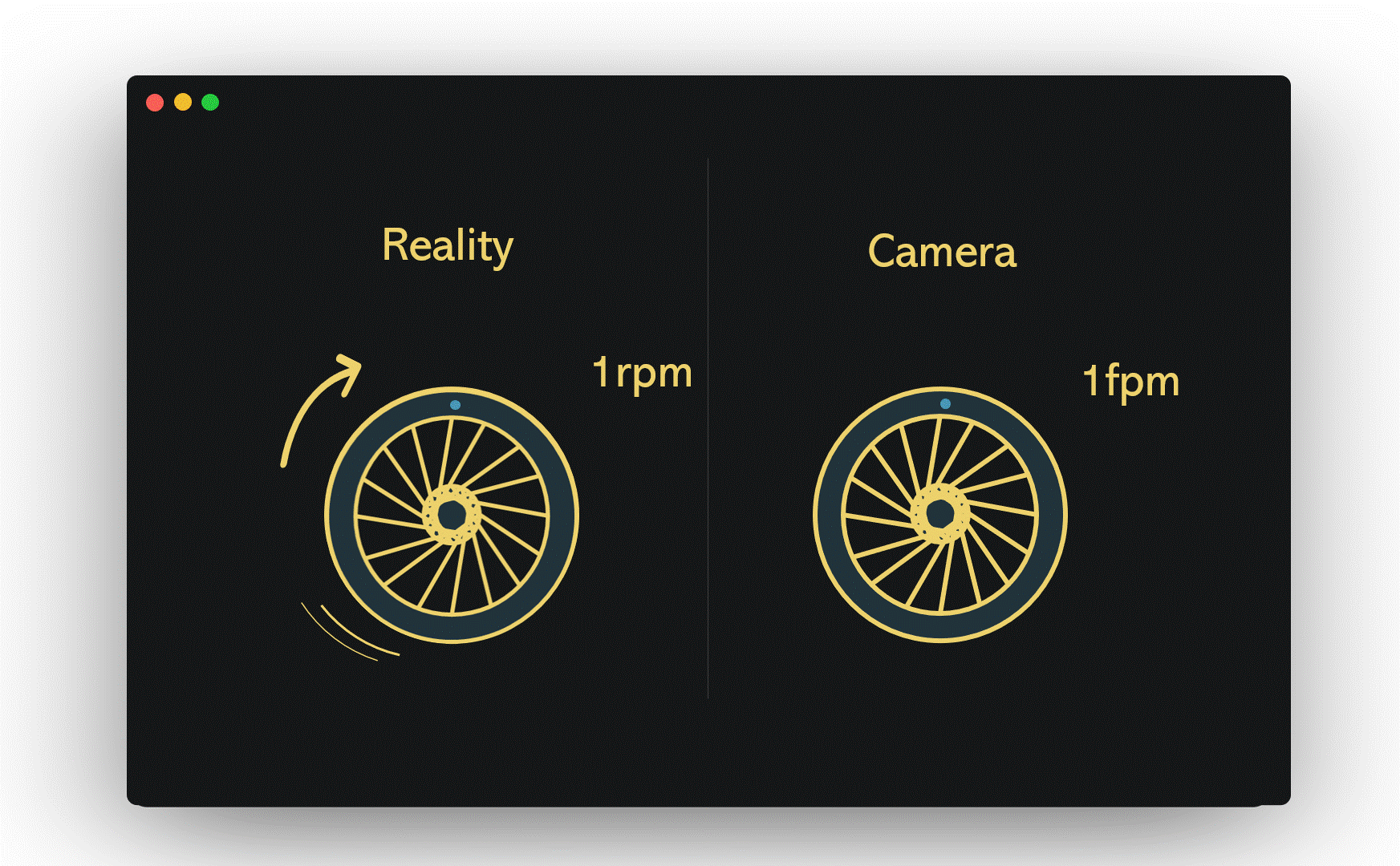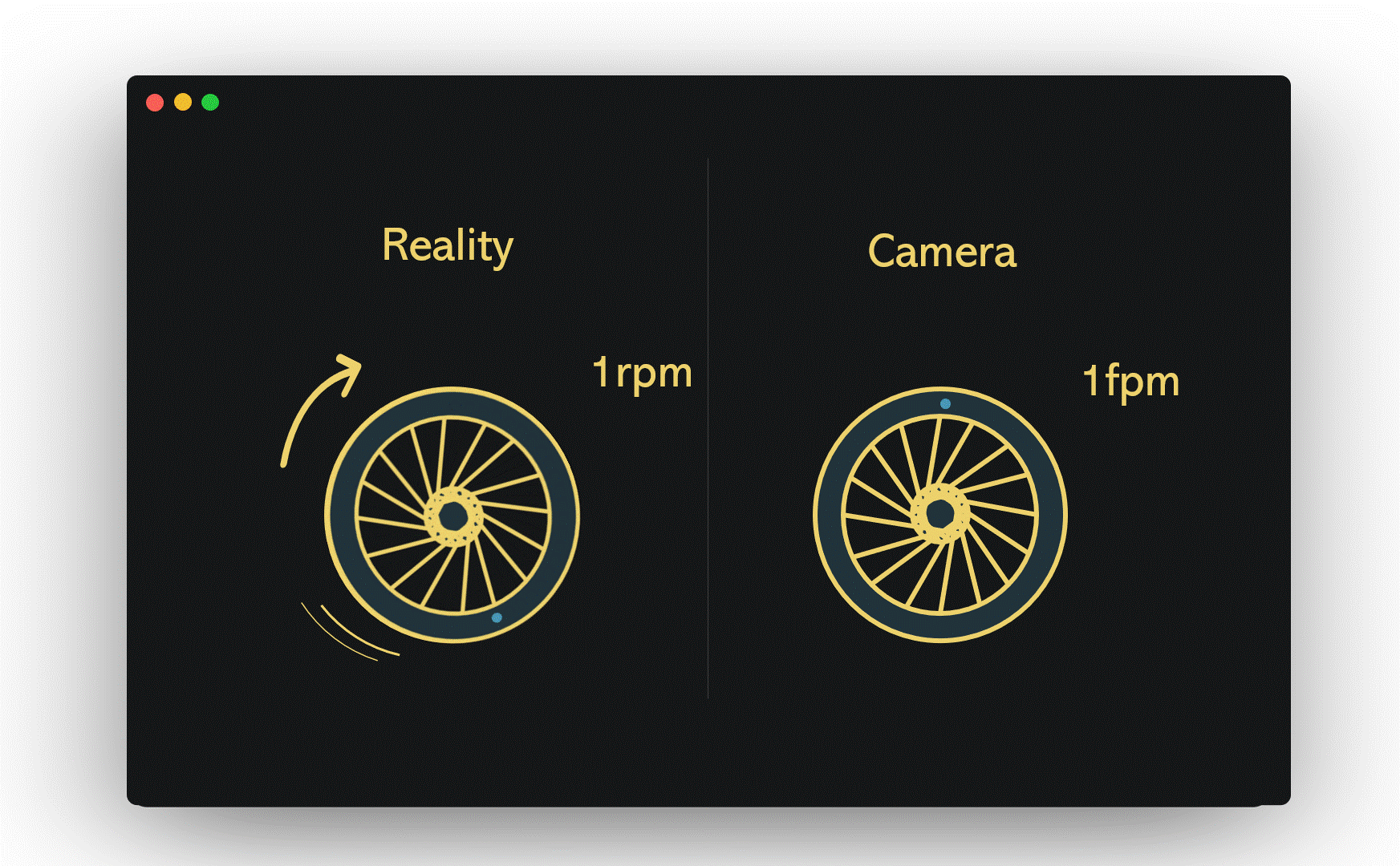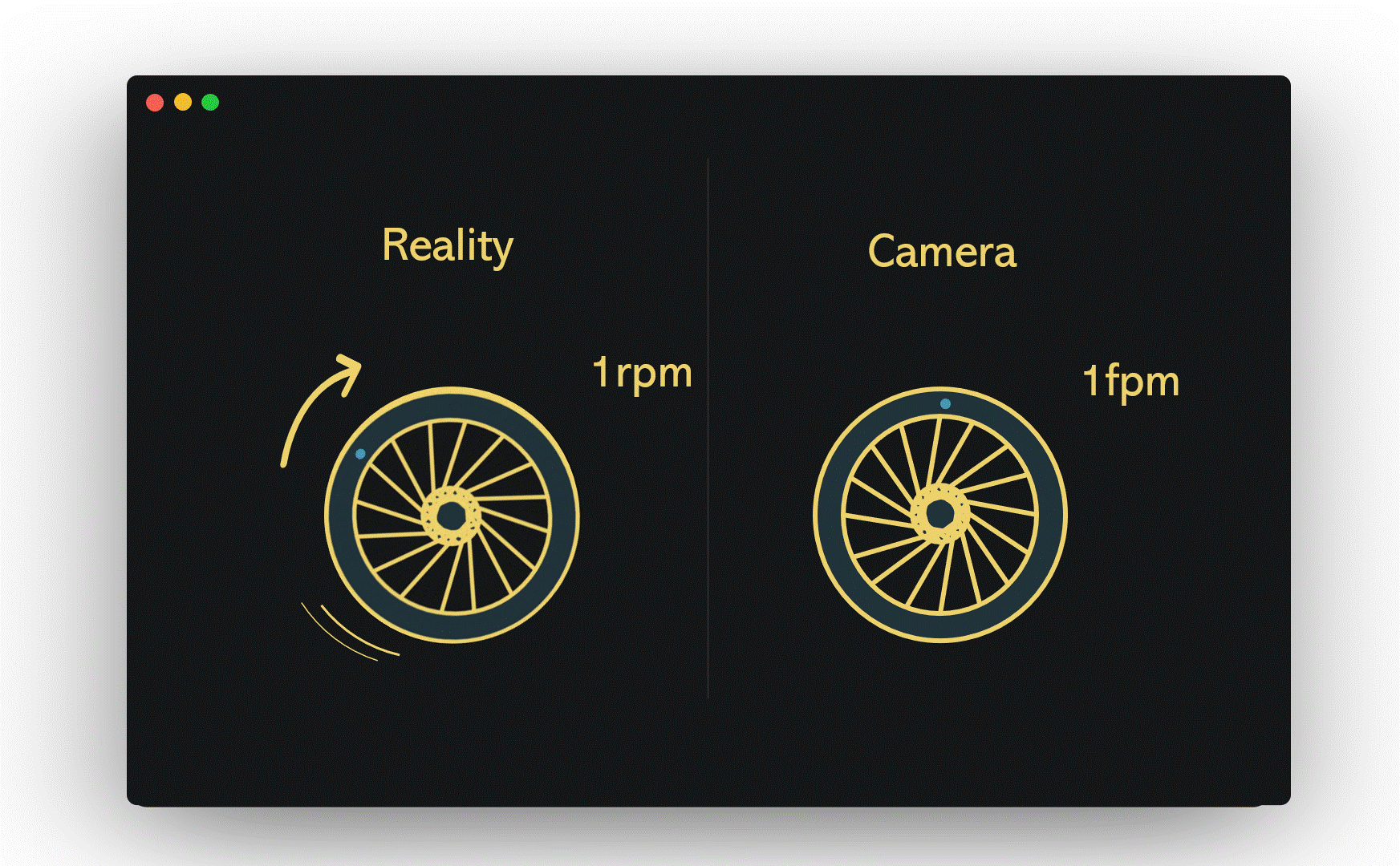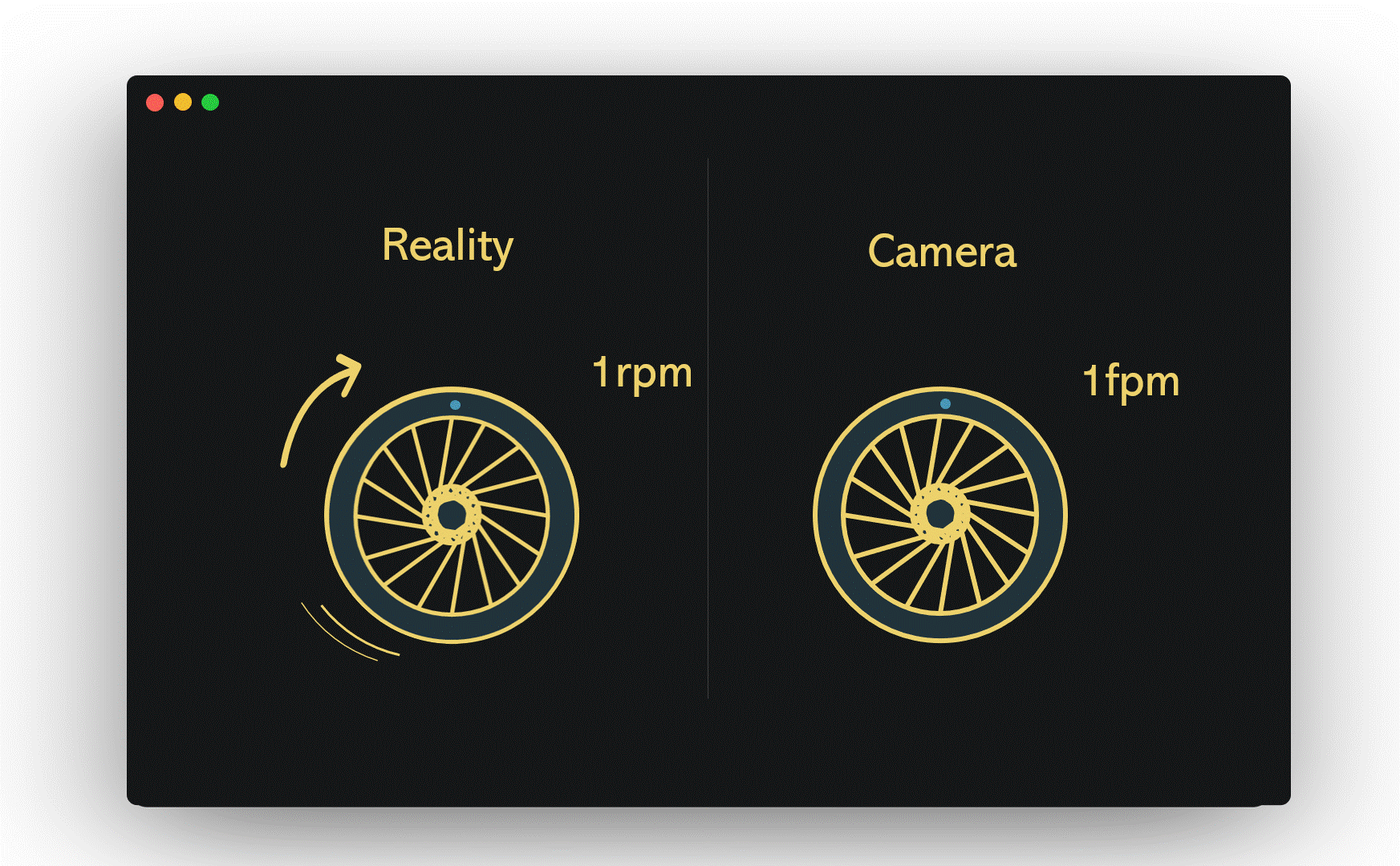
If we maintain the same wheel speed but increase the camera's shutter speed from 1 fpm to 4 fpm, the wheel's motion becomes visible, though the clarity may leave much to be desired.
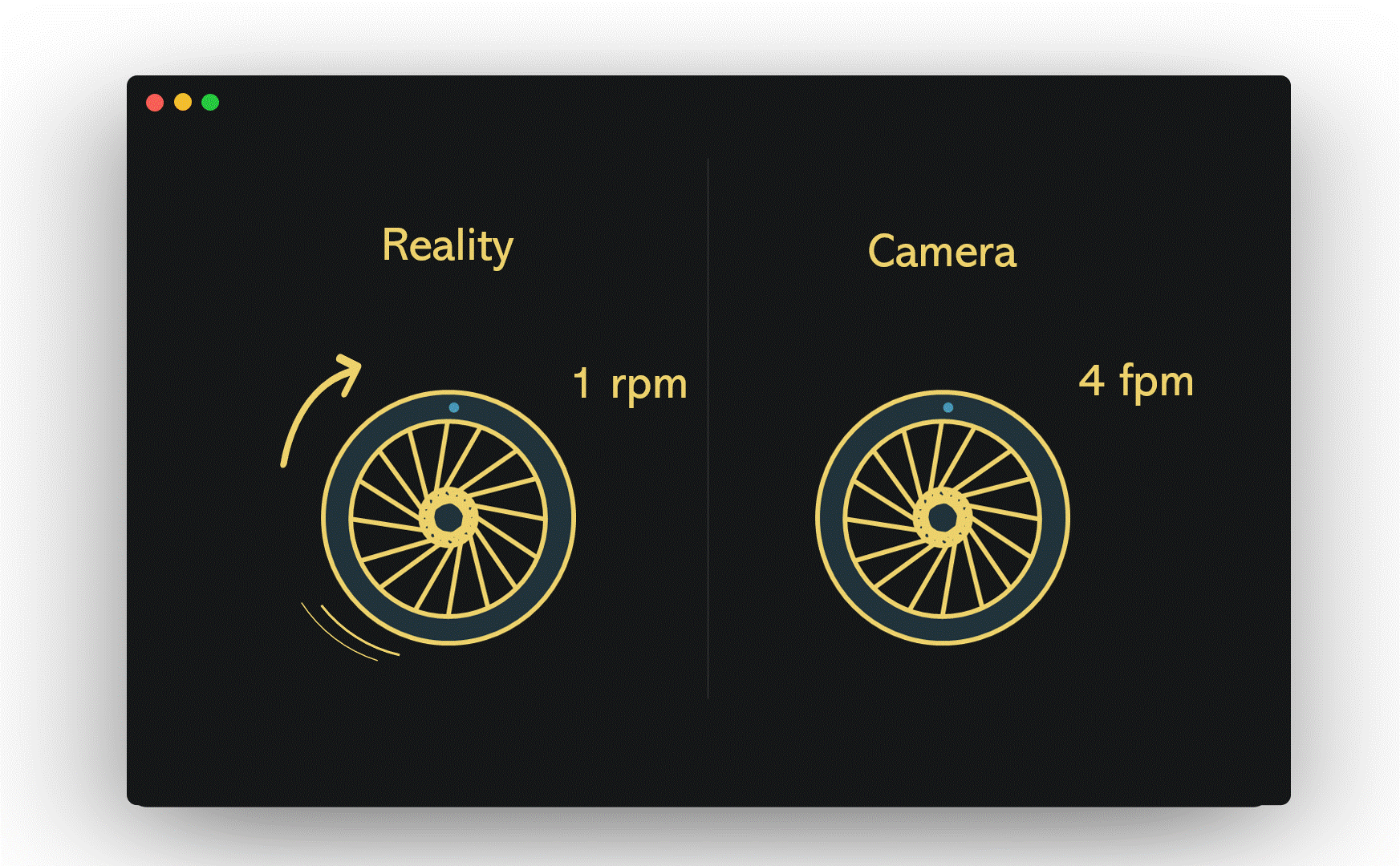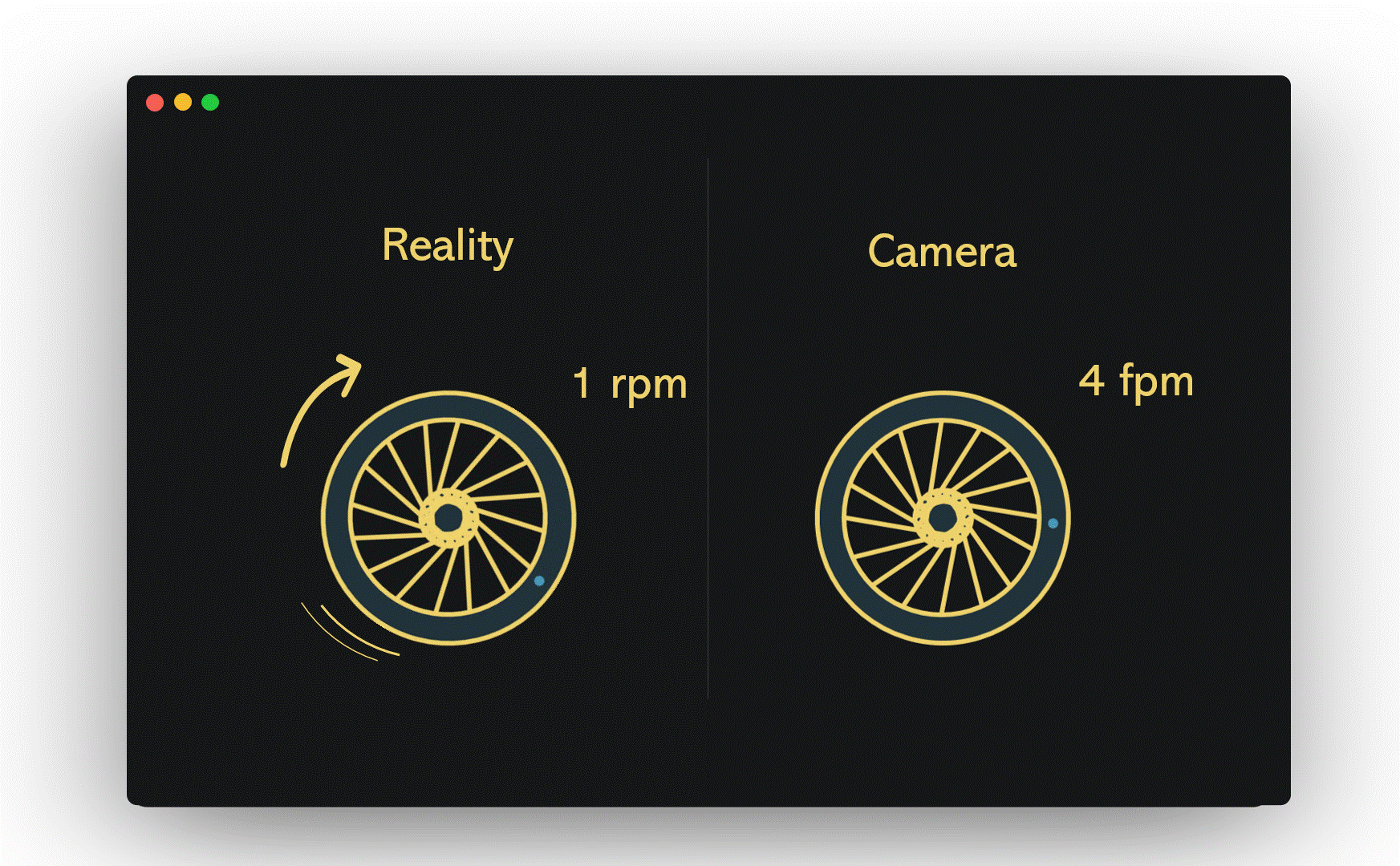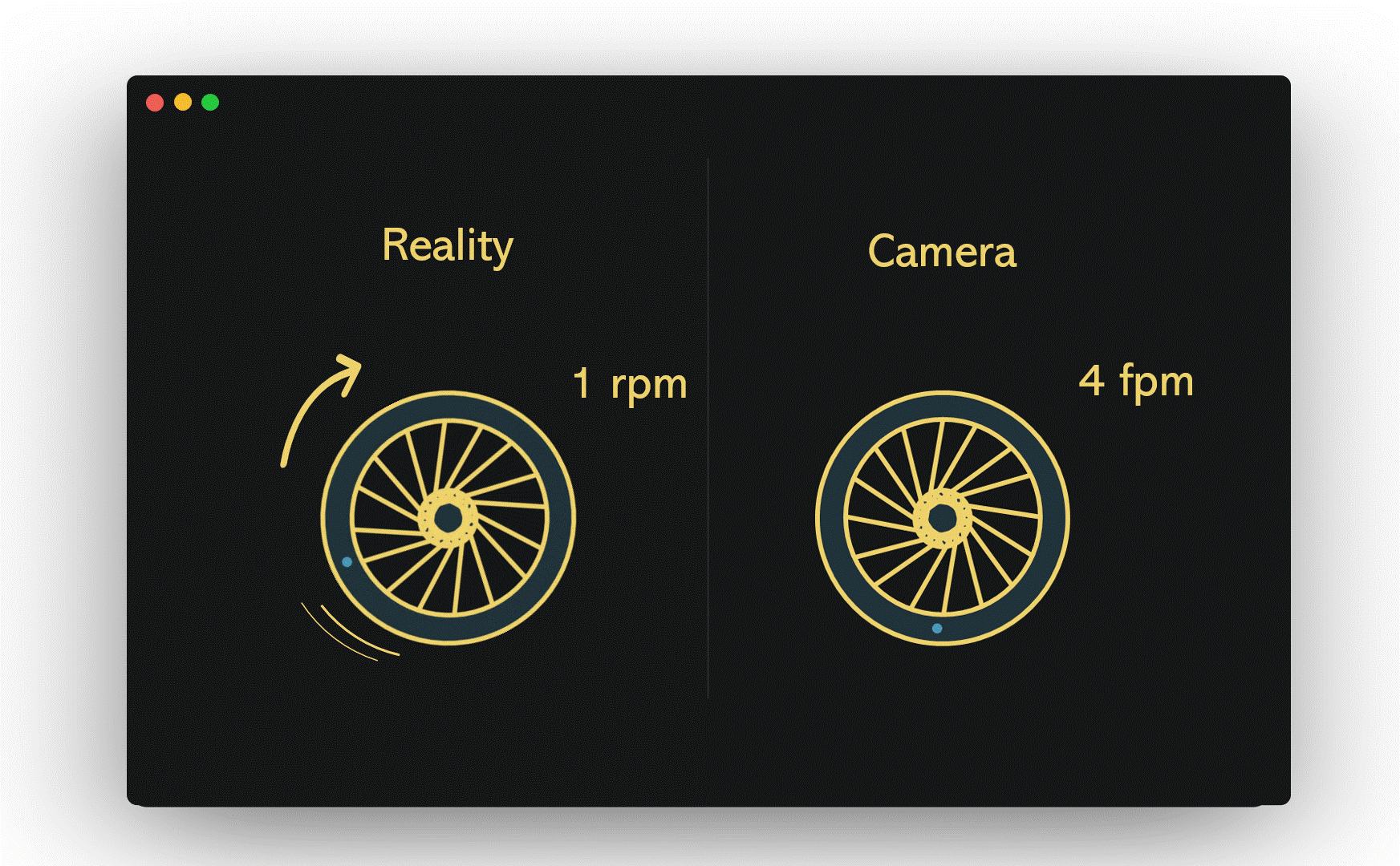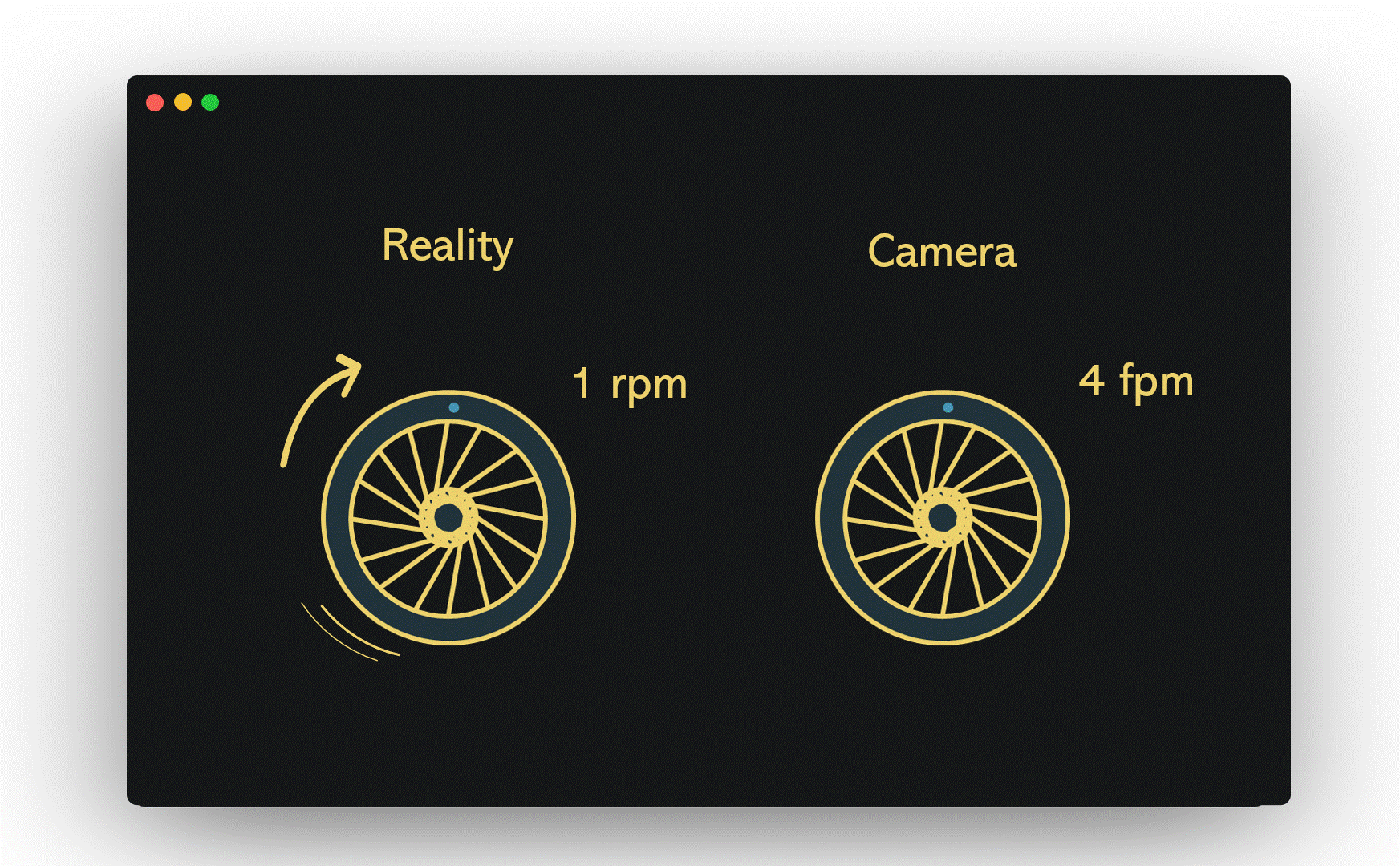
Now, if we accelerate our imaginary wheel to 14 rpm and set the camera's shutter speed to 15 fpm, the wagon wheel effect emerges. Each time the camera captures an image, the wheel is 24 degrees short of completing its full rotation. Consequently, our brains perceive it as rotating 24 degrees counterclockwise rather than completing a full 336 degrees clockwise.
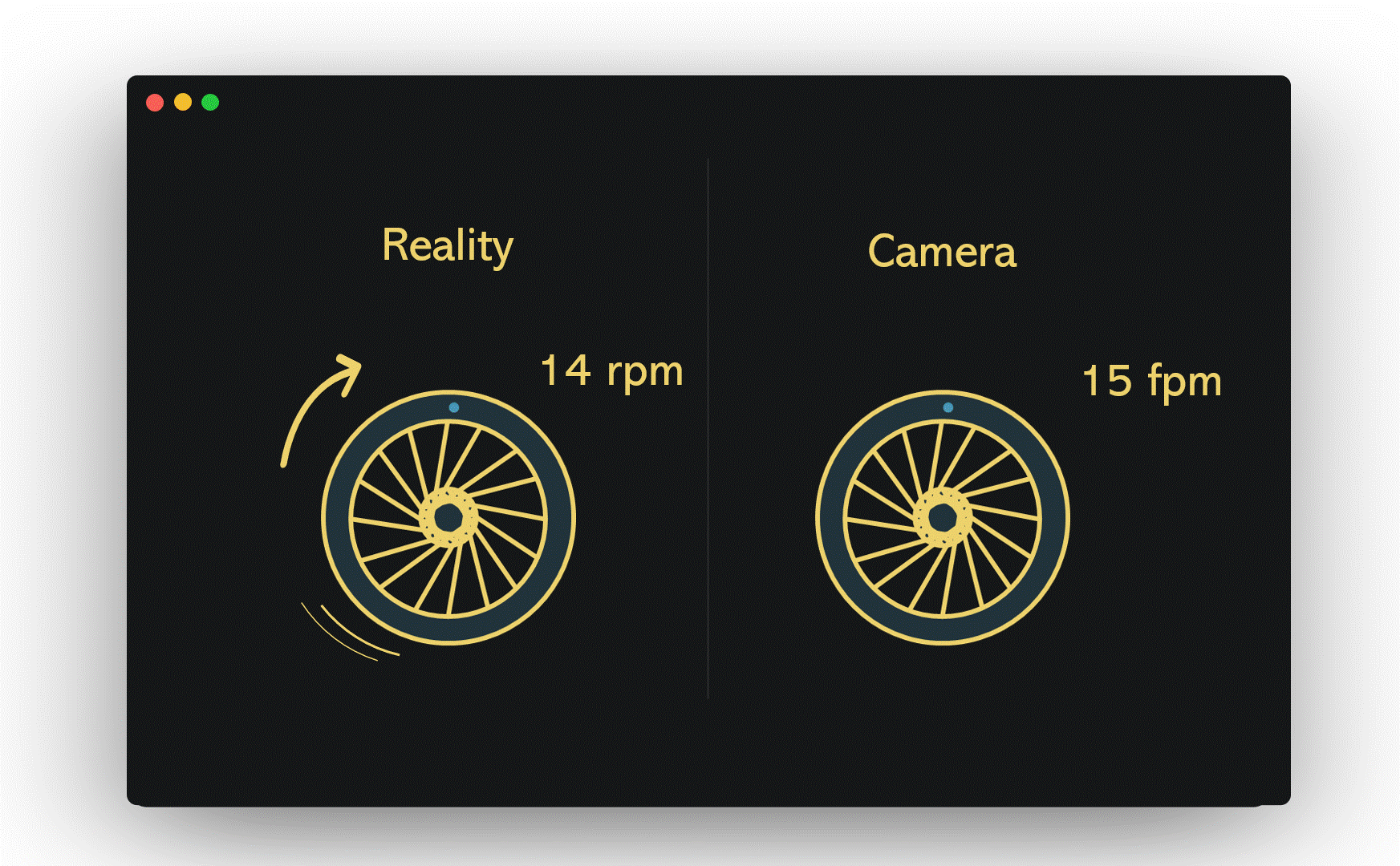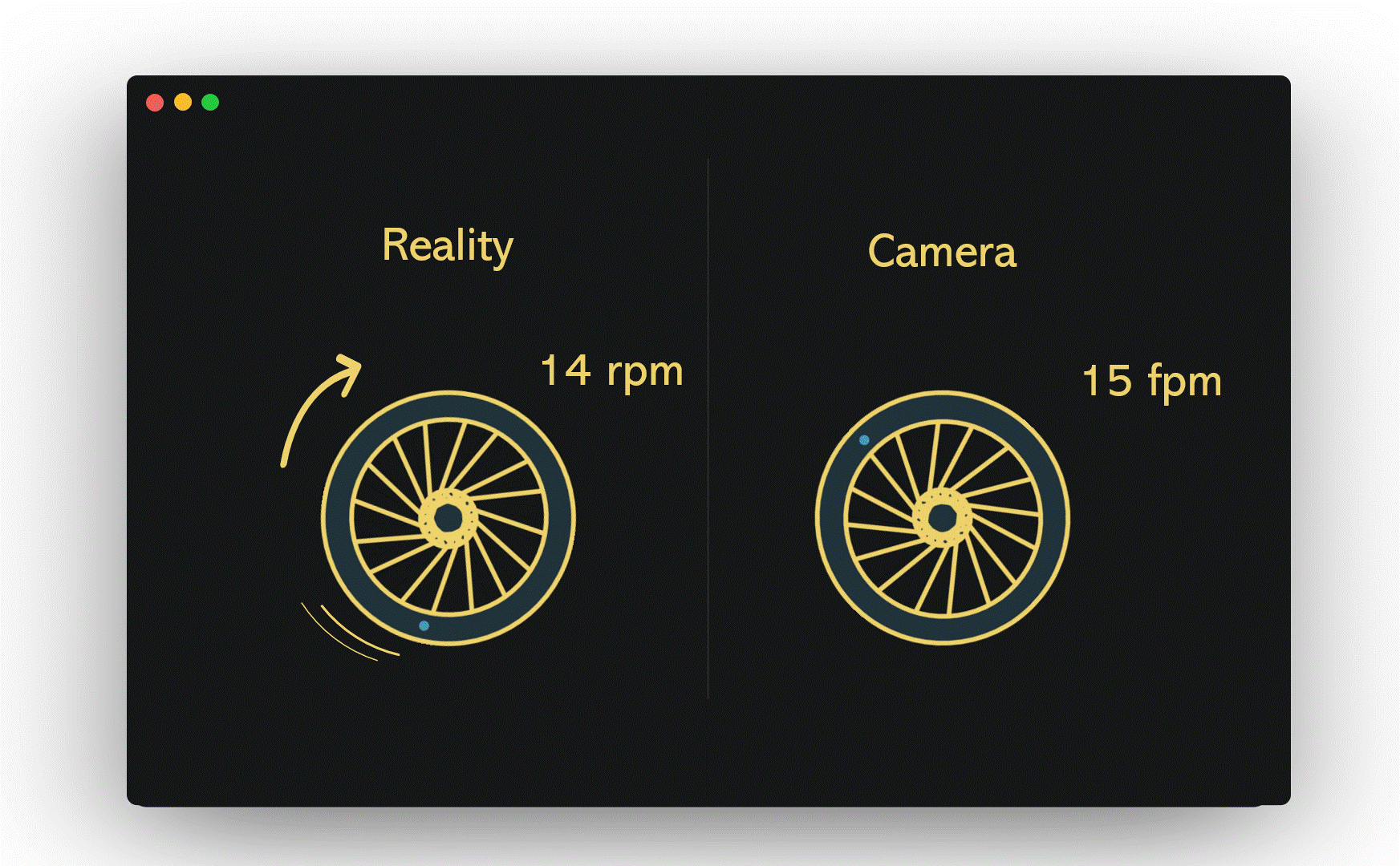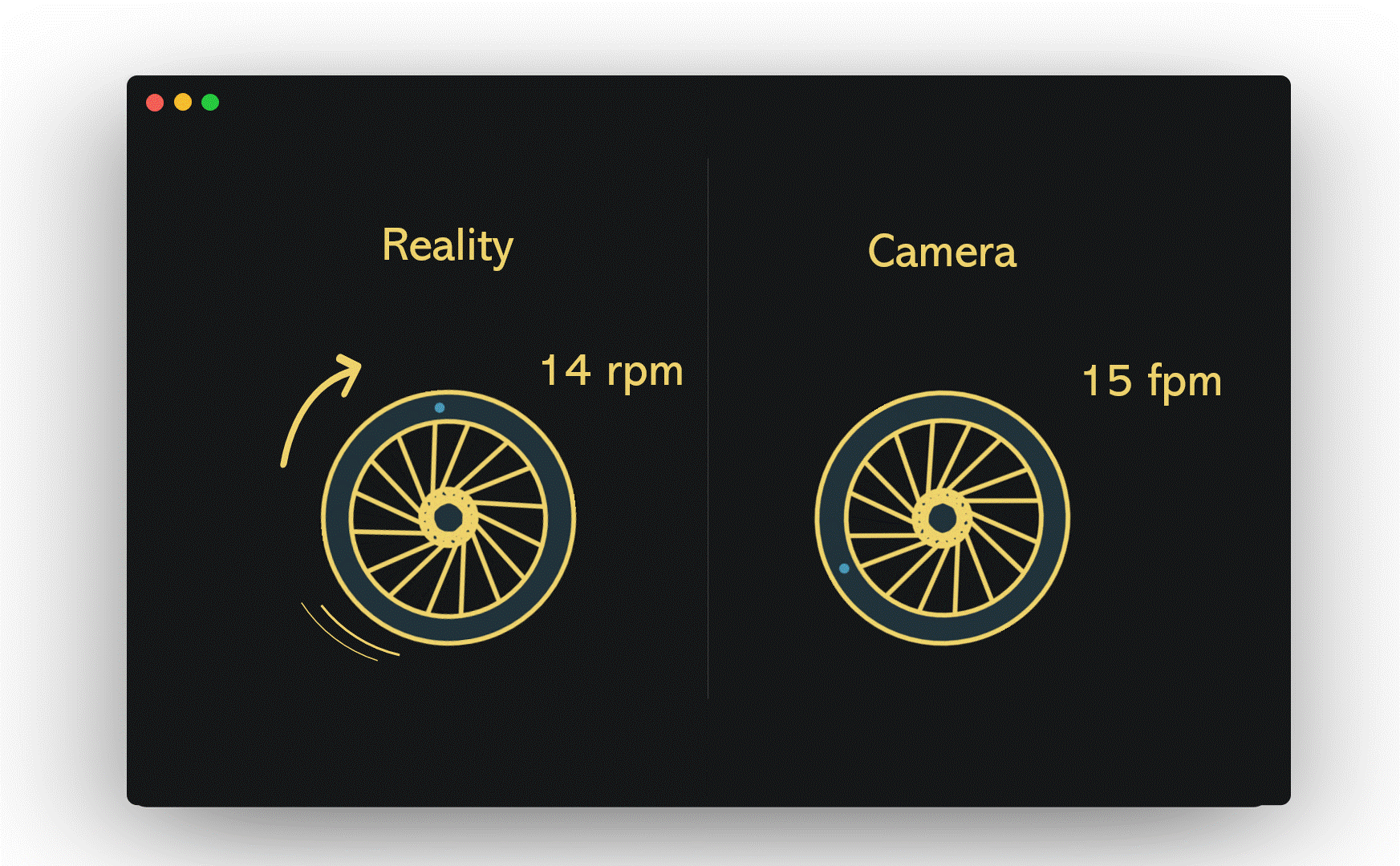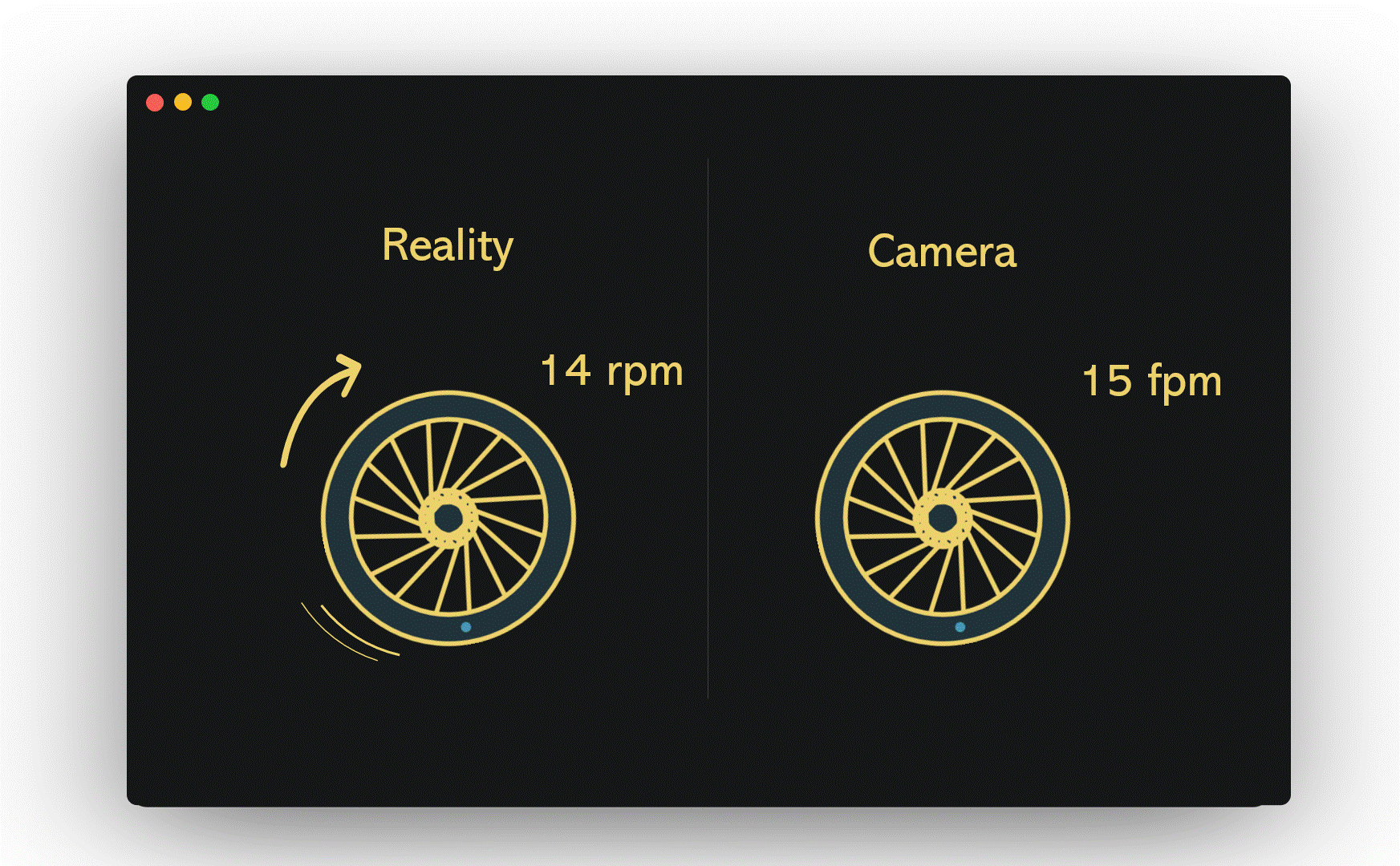
Section 1.2: Delving Deeper into Aliasing
Aliasing generally occurs when a signal is sampled at an insufficient frequency. Sampling involves taking measurements of a continuous signal at regular time intervals, as illustrated below.
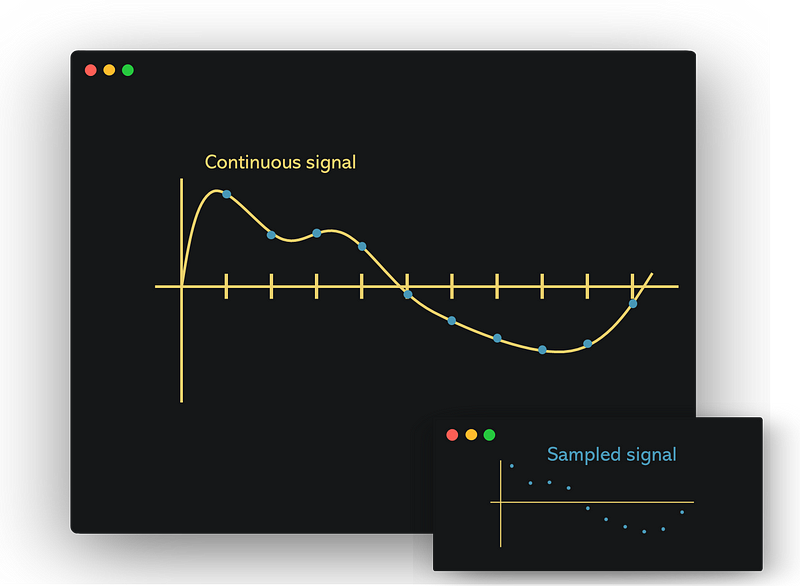
In our analogy, the spinning wheel represents a continuous signal, while the footage captured by the camera acts as the sampled signal. When a continuous signal is sampled, the resulting representation is only accurate within a specific frequency limit. If the original signal contains higher frequency components, these can "alias" back into the lower frequency range of the sampled signal, causing distortions and hindering the accurate reconstruction of the original signal.
In the case of a spinning car wheel, aliasing occurs when the wheel’s rotation frequency exceeds the camera’s frame rate, resulting in insufficient images being captured to accurately depict the wheel’s speed. Essentially, a video is a sequence of still images played in succession to create the illusion of motion.
Chapter 2: Preventing Aliasing
While aliasing might serve some artistic purposes in cinematography, it's typically something to be avoided in most other contexts. To mitigate this, one can apply the Nyquist rate.
The Nyquist rate represents the minimum sampling frequency required to accurately capture and reconstruct a continuous signal (like our spinning wheel) in digital form. According to the Nyquist theorem, the sampling rate should be at least twice the maximum frequency present in the signal. For example, if a wheel spins at 5 rpm, the camera's shutter speed should be no less than 10 fpm. If the wheel were to accelerate even slightly beyond that, it would appear to rotate backward—a demonstration of the theorem’s validity.
The first video illustrates how to draw spinning wheels optical illusions, showcasing techniques that play with perception and aliasing.
The second video takes us through a psychedelic spinning pottery wheel optical illusion, further emphasizing the effects of motion perception.
Exam Question: A Practical Application
To wrap up, let's consider an exam question posed in the second year of engineering at the University of Leuven, Belgium.
A wheel rotates at n revolutions per second and gradually accelerates to 3n/2 revolutions per second while the camera records at 6 fps. Initially, the wheel seems stationary, then appears to rotate in one direction, then the opposite, and finally slows down to a stop again. What possible values can n take?
To solve this, we start by analyzing the two stationary states. We can define the camera's frequency as 1/tau (1/? = 6), indicating that the camera captures a new frame every ? seconds. The angle the wheel turns in tau seconds can be calculated as follows:
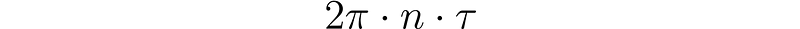
At n rotations per second, the wheel appears stationary, meaning that each time a frame is taken, the wheel has completed one or more revolutions. Thus, the angle covered in tau seconds must be a multiple of 2π radians.
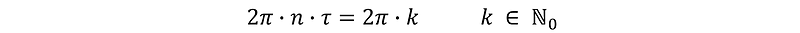
The same logic applies for 3/2 n revolutions per second.
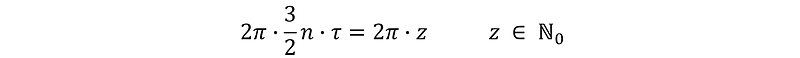
By applying (? = 1/6), we derive:
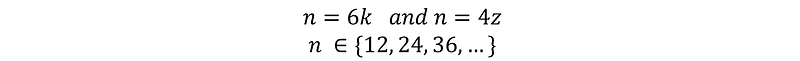
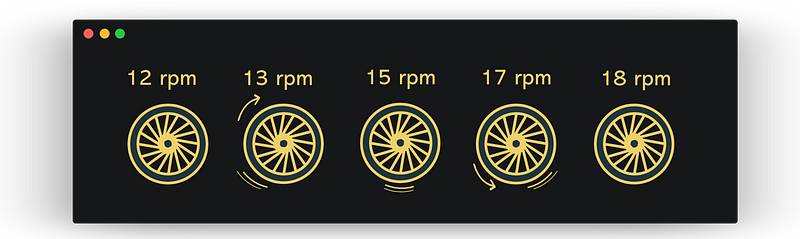
Let’s examine n = 12 for potential outcomes. With the wheel spinning at 12 rotations per second, the camera captures a frame every two rotations, making the wheel appear stationary. As it accelerates to 13 revolutions per second, the wheel begins to rotate in one direction. When it reaches 15 revolutions per second, the wheel completes two and a half rotations between frames, leaving the camera unable to discern its direction. Further acceleration to 17 rotations per minute causes the wheel to appear to rotate in reverse. Finally, at 18 rotations per minute (3/2 n), the wheel completes three revolutions between frames, appearing stationary again. Thus, n = 12 stands as a valid solution.
For n = 24, the results differ slightly. The wheel first appears stationary, then rotates in one direction at n = 25, reaches a turning point at n = 27, and seems to spin in the opposite direction at n = 29. It returns to a stationary state at n = 30, but since we haven't yet reached 3/2n (= 36), this cycle of stillness and motion repeats twice. Hence, n = 24 does not present a valid solution.
Ultimately, the only valid solution is n = 12.
Final Thoughts
The backward-spinning wheels on a forward-moving car may not be as enchanting as they seem. By employing the analogy of a spinning wheel and a camera, we have gained a clearer understanding of aliasing and its implications. Although comparing a spinning wheel to a continuous signal might initially appear abstract, the parallels are substantial. This analogy can also be utilized to confirm the Nyquist rate.
But What is Light?
It took a genius to figure it out
www.cantorsparadise.com
We Now Know 62.8 Trillion Digits of Pi.
But should we even care?
www.cantorsparadise.com