Chapter 2: Socratic Dialogue Begins

Socrates: Have you had any training in Olympiad Mathematics, young one?

Boy: No, Socrates, I am just a simple slave without education.

Socrates: Just as I thought. Nevertheless, you can tackle this Olympiad question. It may appear daunting, but allow me to clarify the problem, and you shall find the answer.

Socrates: Imagine we have eight coins: four made of aluminum and four made of bronze. I will line these coins up. Now, take the 4th coin from the left along with the chain of like coins that includes it, and move this chain to the start of the row.

Keep repeating this process and observe whether the leftmost four coins become uniform in type.

Boy: They do.

Socrates: Excellent. Now, let’s generalize the concept to any number of coins (n). Instead of always taking the 4th coin, we can select any position (k) as special. Your task is to identify all pairs (n, k) such that the leftmost n coins turn out to be of the same type, regardless of the initial arrangement.

Boy: I’m a bit lost.

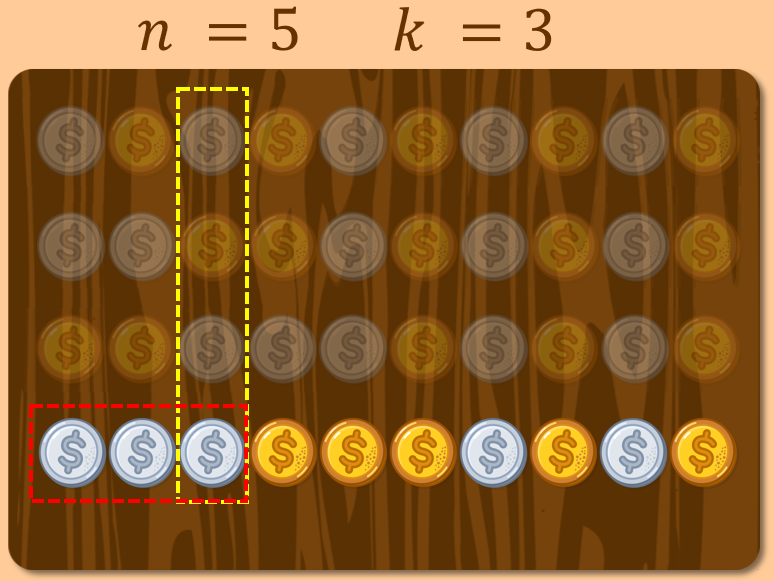
Socrates: That’s perfectly fine. Let's try a different example: set n = 5 and k = 3. Arrange the coins in any order you choose and repeat the process by moving the entire chain containing the 3rd coin to the beginning.

Boy: This time, three aluminum coins are stuck at the left side and cannot move. No further changes will occur.

Socrates: Hence, the leftmost five coins do not become uniform.

Boy: Correct.

Socrates: Therefore, you have shown that n = 5, k = 3 is not a solution. What about n = 5, k = 4?

Boy: I believe that also isn’t a solution. I could arrange the four bronze coins at the start, with the fifth bronze coin separated.

Socrates: And should I give you 100 bronze and 100 aluminum coins, would n = 5, k = 99 be a viable solution?

Boy: It would not be. I would place 99 aluminum coins first, followed by 99 bronze coins, and then one aluminum and one bronze coin. The arrangement would remain static, and the leftmost 100 coins wouldn't become uniform.

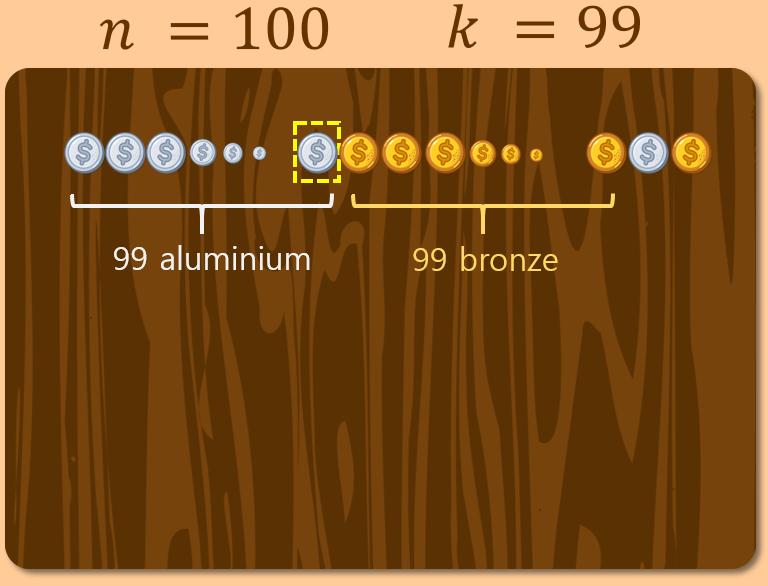
Socrates: From your reasoning, does it not appear that for a pair (n, k) to be valid, k must be at least n?

Boy: Certainly.

Socrates: Well done! However, our objective is to find pairs (n, k) that work. While we have dismissed some pairs, we have yet to uncover valid pairs.

Boy: Except for n = 4, k = 4, which we validated earlier.

Socrates: Indeed… yet while we showed one arrangement for n = 4, k = 4, we didn’t prove it for any arrangement of coins.

Boy: That worked again! I am convinced, Socrates, that no matter how we arrange the coins, we will always end up with four identical coins at the left. I am confident that n = 4, k = 4 is indeed a solution.

Socrates: Can you articulate why that is?

Boy: The chains merge continuously, growing longer until only two chains remain: one aluminum and one bronze.

Socrates: A solid explanation. Now let’s refine it. Does the chain that moves grow longer with every move?

Boy: Sometimes it combines with another like coin, but not always.

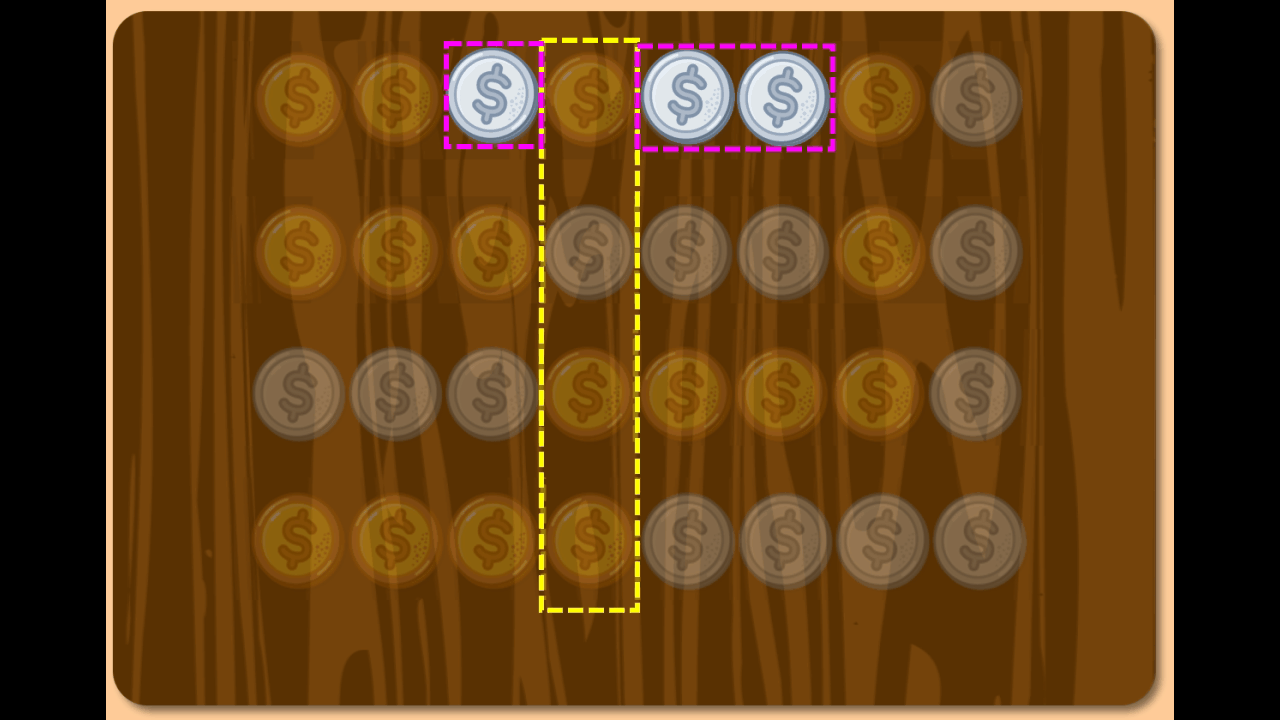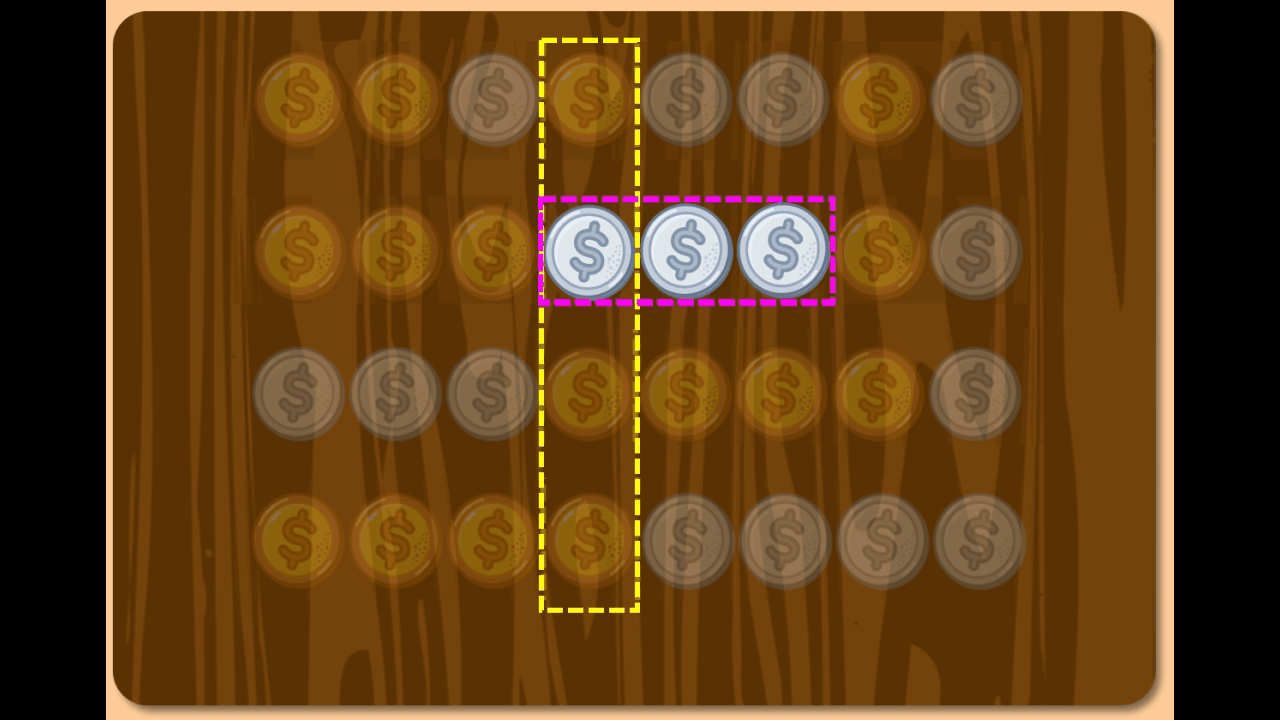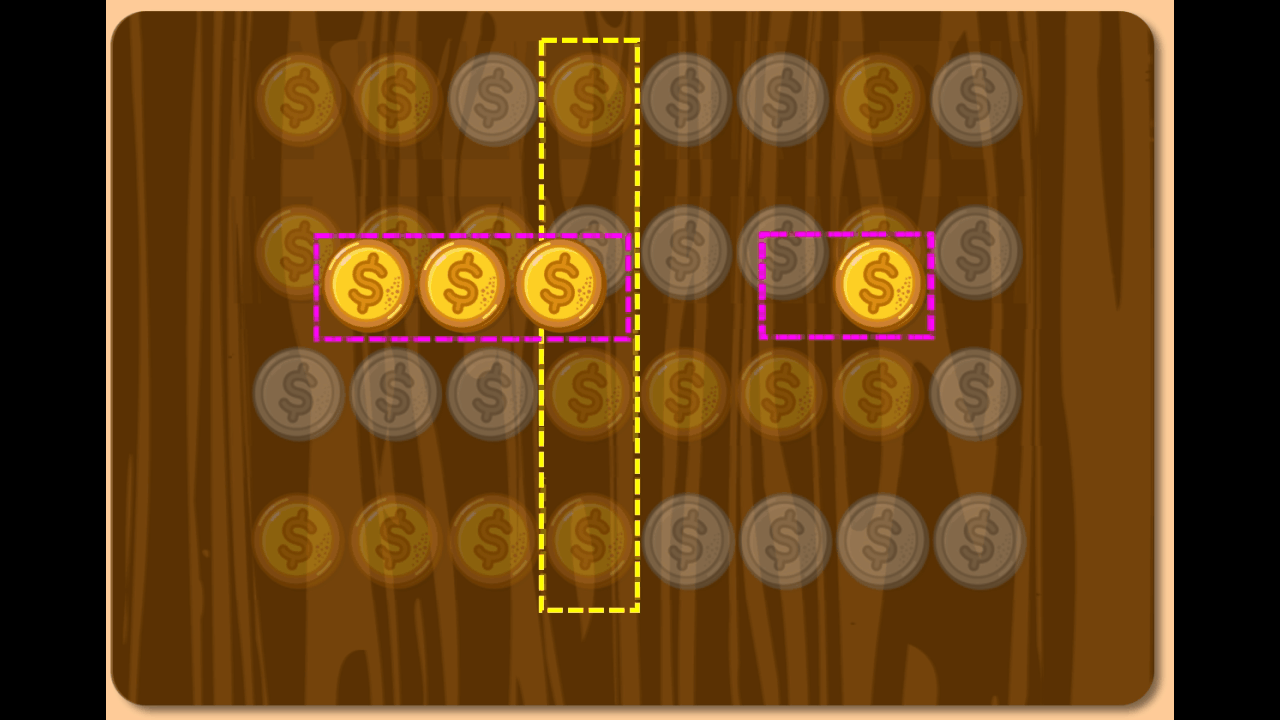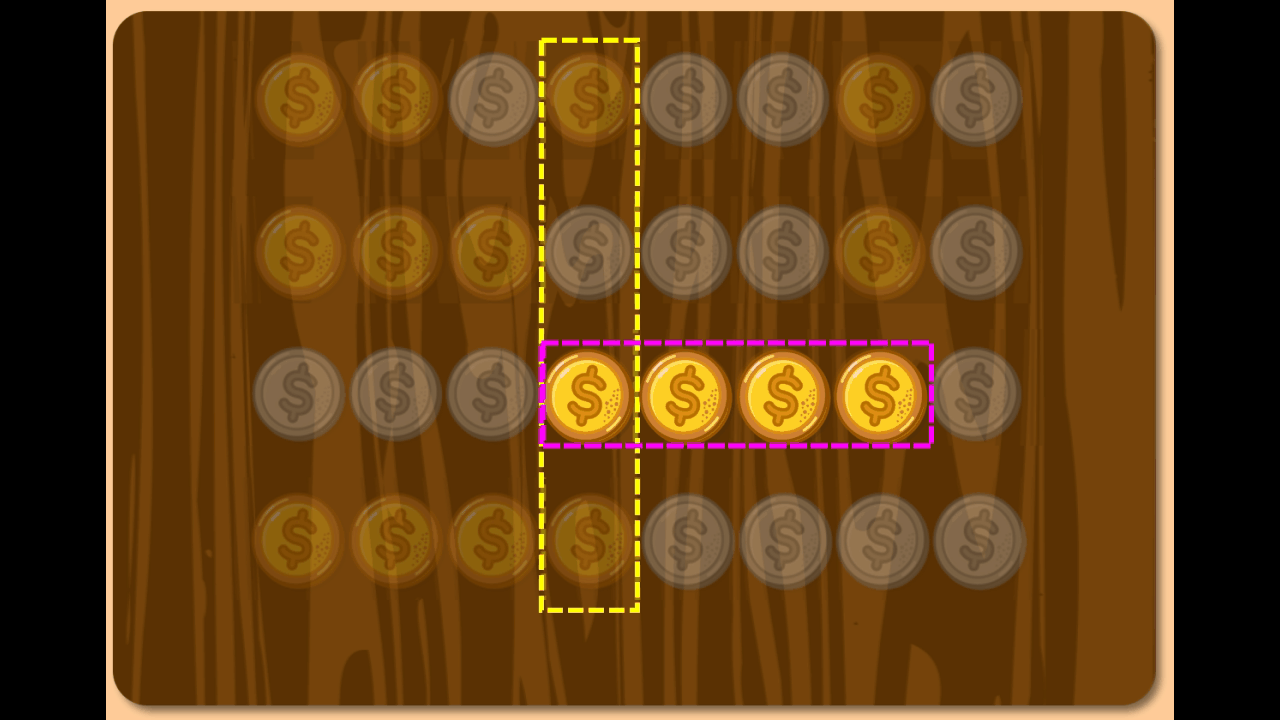
Socrates: Correct. And what of the remaining chains?

Boy: The others?

Socrates: Yes, do those chains combine with others?

Boy: Ah… the coins beside the removed chain always merge to form a longer chain.

Socrates: And can you explain why this happens?

Boy: Because the two surrounding coins must be of the same type… opposing the removed chain.

Socrates: Right. Now tell me, can any chain split into smaller chains during a move?

Boy: We always take an entire chain and move it, so no existing chain can split.

Socrates: To summarize: With every step, no chain can split, and any removed chain must combine with others to create a longer chain. What conclusion follows from your observations?

Boy: I see! Ultimately, all chains must combine into two: one aluminum and one bronze.

Socrates: Precisely, and when n = 4, the removed chain must have at least one coin adjacent on both sides because…

Boy: If the chain stretched from the 4th position to the end, the leftmost four coins would all match.

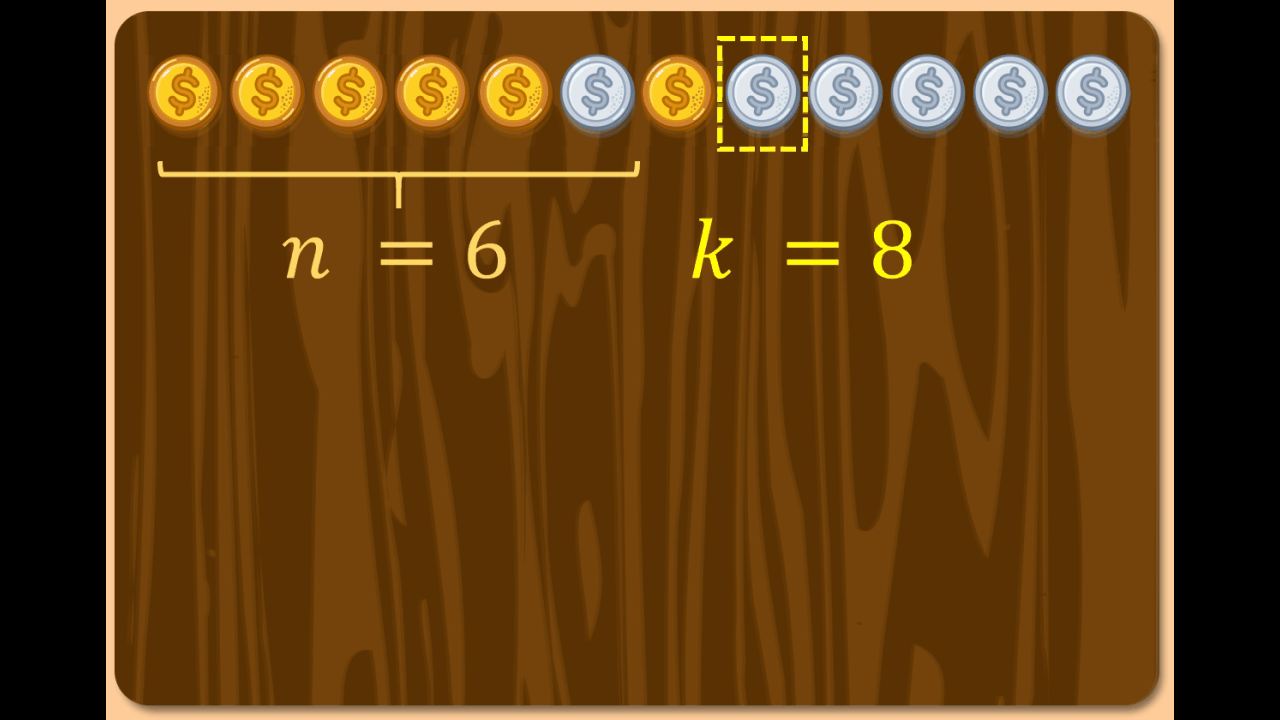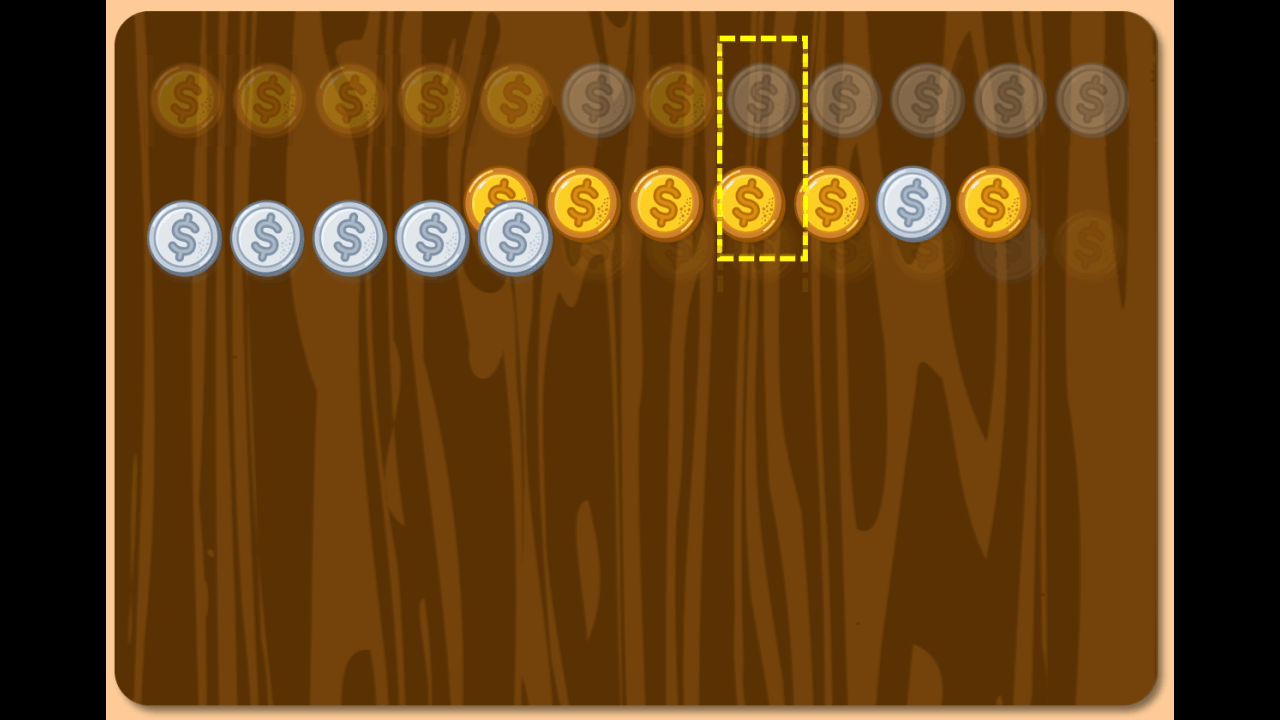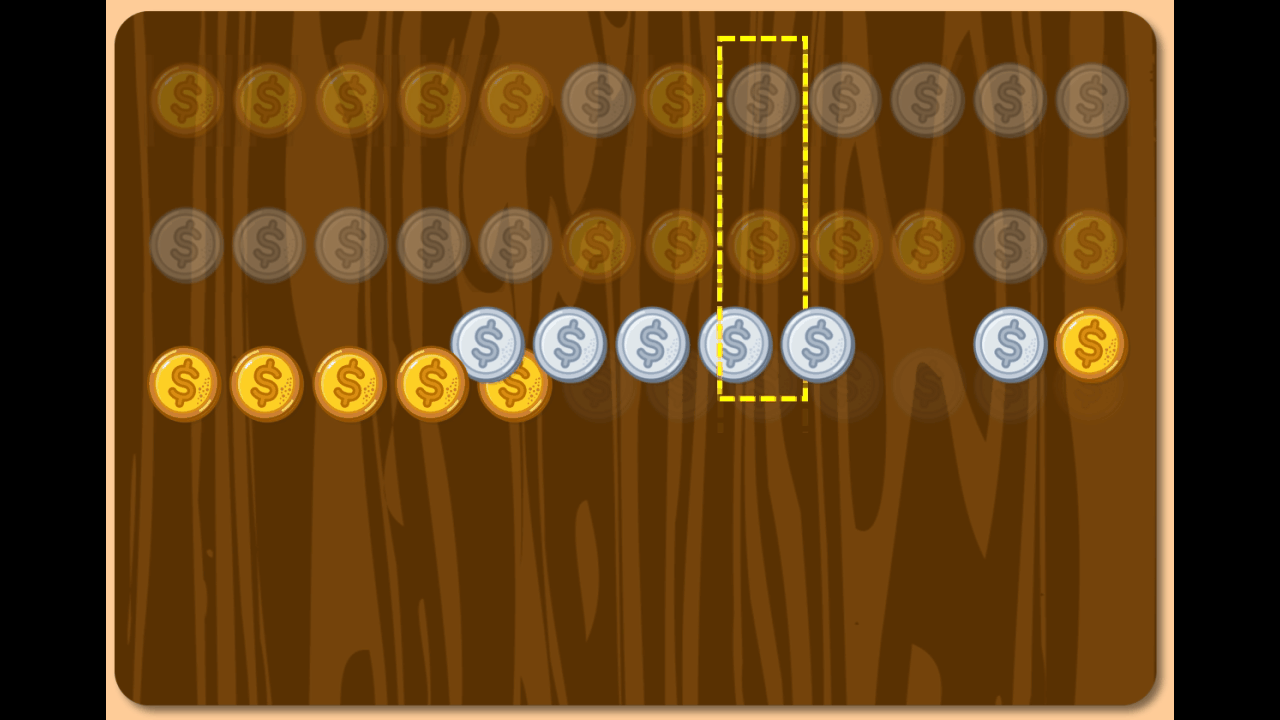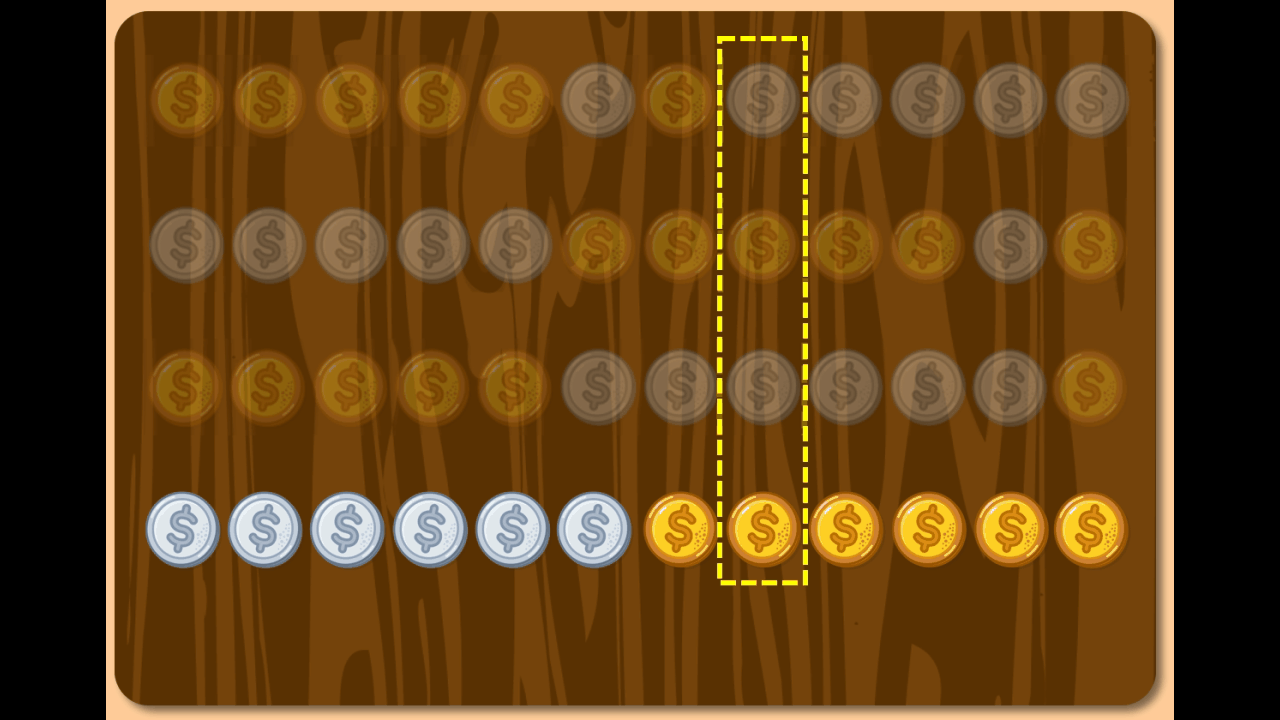
Socrates: Exactly, and this logic holds when n = k as well. What about n = k + 1?

Boy: n = k + 1 should also yield a solution. If the chain reached the row's end, the leftmost n coins must match.

Socrates: So do you believe all k values equal to or greater than n will yield solutions?

Boy: Let me test another case...

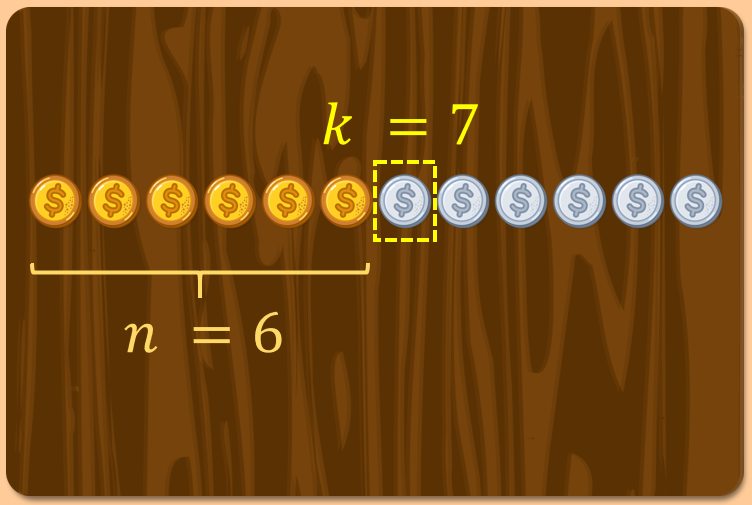
Boy: Okay, n = 6, k = 8 works. Even though a chain might extend to the end, not every chain can. The number of chains will decrease until only two remain.

Boy: The same logic applies for n = 6, k = 9. A chain would need four coins to reach the end, leaving a shorter chain in the middle.

Socrates: Your reasoning is sound.

Boy: But with n = 6, k = 10, chains could form of length three.

Socrates: Correct. All chains would reach the end, preventing any reduction.

Are you now prepared to articulate the solution to our problem?

Boy: I believe so, Socrates. The solution pairs are (n, k) where k is at least as large as n but does not exceed three halves of n.

Socrates: That’s accurate… in certain cases. However, consider a scenario where n is odd.

Boy: Alright, let me try n = 5. Three halves of n would be 7.5, meaning n = 5, k = 8 could also work, as chains of at least three would reach the end.

Thus, for odd n, k must be less than one above three halves of n.

Socrates: You are correct, young one. Congratulations.

Let us express this algebraically for those who prefer a formal approach:

For k values greater than n, a solution exists as long as not all chains from the k-th position extend to the right end of the row. This length is (2n - k + 1), and at least two chains must be present, thus:

2(2n - k + 1) > n

4n - 2k + 2 > n

3n > 2k - 2

k < 3n/2 + 1

Socrates: How do you feel, having tackled this Olympiad mathematics problem?

Boy: Exhausted! But fulfilled. I will sleep soundly tonight!

Socrates: Thank you, young one. You have demonstrated that anyone who can communicate, reason, and has the determination can solve such challenges.

Boy: And only with a wise and patient teacher! Thank you, Socrates.