Daily Insights into Scientific Python

Common and unique challenges are resolved using tools like Numpy, Sympy, SciPy, and Matplotlib.

Section 1.1: Understanding Fourier Series

Consider a function defined over the interval [a, b].

Fourier analysis asserts that we can express this function as an infinite series of complex exponentials (or alternatively, sines and cosines):

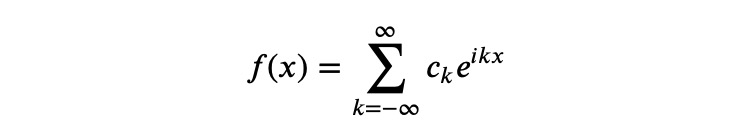
Moreover, it provides a method to compute the coefficients using the following integral:

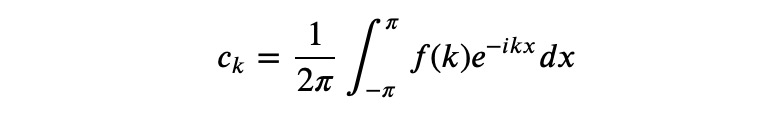
Let’s implement this using Sympy in a Jupyter notebook by defining our symbols:

For convenience, it’s beneficial to encapsulate the Fourier coefficient calculations within a function:

Since we cannot compute an infinite number of coefficients, we will set a limit. Let's consider k values ranging from -3 to 3:

Our approximation for f(x) thus becomes:

Although this is a rough representation of the original function, refining our approach by including more k values (e.g., 2 * 30 + 1) yields a much closer approximation:

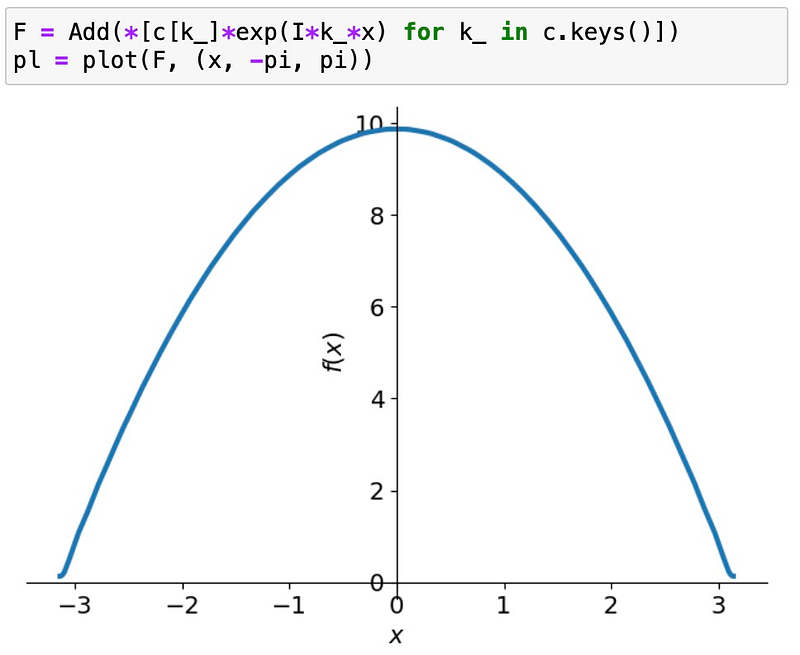
However, if we extend the function's domain and visualize the Fourier approximation beyond the original bounds:

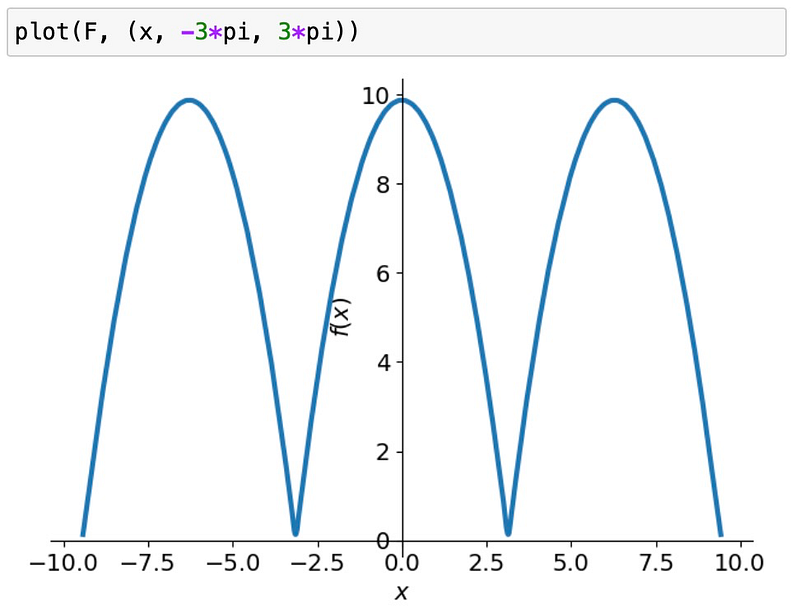
This illustrates a characteristic of the Fourier series—repetition beyond the defined interval. If your interest lies solely within the original bounds, this is acceptable.

Section 1.2: Differentiating with Fourier Series

Fourier series can do more than just approximate functions. By applying differentiation to the Fourier series definition, we can interchange the differentiation operation with summation:

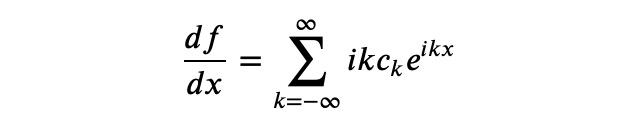
Rather than taking the derivative directly with respect to x, we can multiply each Fourier coefficient by iω and sum them up. Let’s explore this:

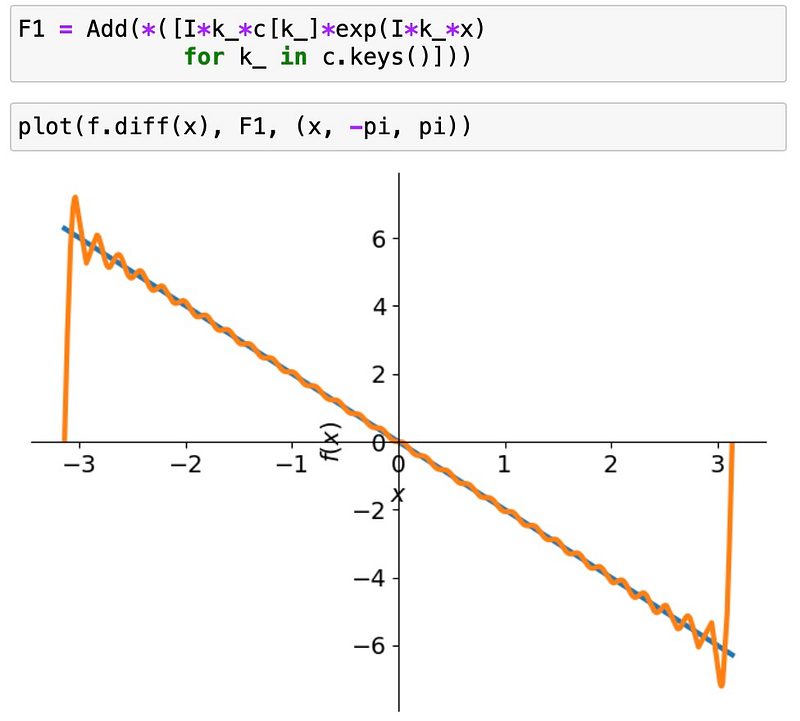
The approximation seems adequate within the interval, but noticeable deviations appear at the boundaries, known as the Gibbs phenomenon. This effect manifests with abrupt changes in the function, leading to oscillations near the edges. The Fourier series assumes periodicity beyond the interval, which influences this behavior. As we increase the number of terms (more k values), the approximation improves, although the oscillations do not completely vanish. The amplitude of the Gibbs phenomenon remains relatively constant despite adding more terms, suggesting that Fourier series are most effective for functions that smoothly transition at the interval's edges.

So, why consider using Fourier series for differentiation? In practice, we usually do not. However, this method illustrates a fundamental principle of spectral methods: differentiation can effectively be replaced by multiplication. This concept is particularly advantageous in solving partial differential equations, a topic I will address in a future article. Stay tuned, and thank you for reading!