Chapter 1: Introduction to the Algebra Challenge

Welcome to the fourth installment in our series focused on tricky algebra problems. This challenge presents a system of equations with two unknowns, x and y, which are restricted to real numbers. You are provided with the following equations to solve:

1. x² + y² = 7
2. x³ + y³ = 10

Your objective is to determine the value of the equation:

x + y = ??

Difficulty Alert:

This problem may require extensive methods to solve, and achieving a concise solution will necessitate familiarity with some relatively advanced mathematical concepts.

Spoiler Alert:

If you're eager to solve this on your own, I suggest pausing your reading and attempting it first. Afterward, feel free to return for a detailed discussion of the solutions.

Chapter 2: Analyzing the First Equation

Let's introduce a new variable to represent the sum of x and y:

x + y = k

Starting with the first equation:

x² + y² = 7

Using the binomial square formula, we can rewrite the left side as:

x² + y² = (x + y)² - 2xy

This leads us to a new equation, which we will refer to as equation A.

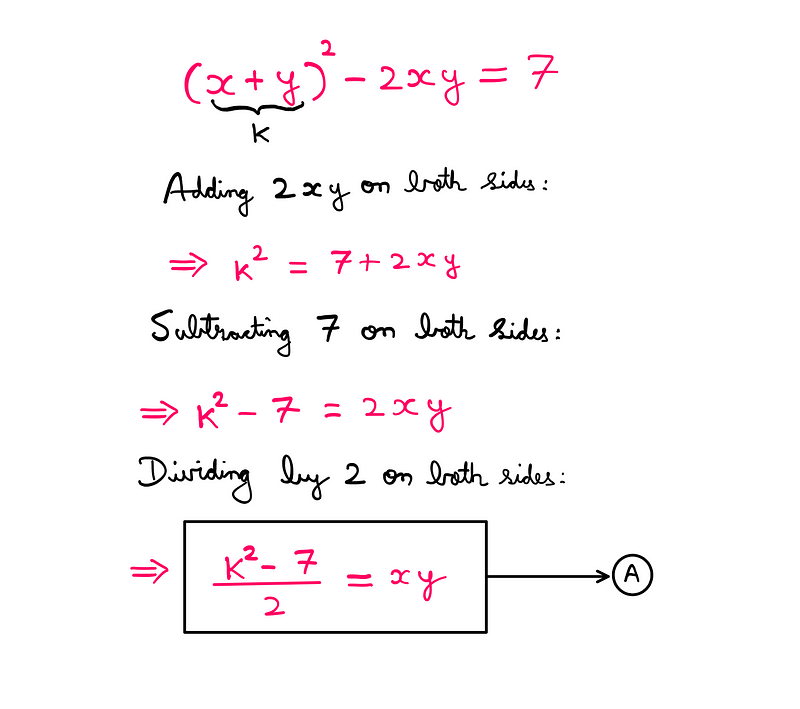
Chapter 3: Exploring the Second Equation

Now, let’s turn our attention to the second equation:

x³ + y³ = 10

Utilizing the binomial cube formula, we can express this as:

x³ + y³ = (x + y)³ - 3xy(x + y)

This gives us a second equation, which we'll call equation B.

Chapter 4: Formulating the Cubic Equation

By combining equations A and B, we derive a cubic equation that we will work to solve.

Chapter 5: Solving the Cubic Equation

To tackle this cubic equation, I generally start with algebraic manipulation to simplify the expression.

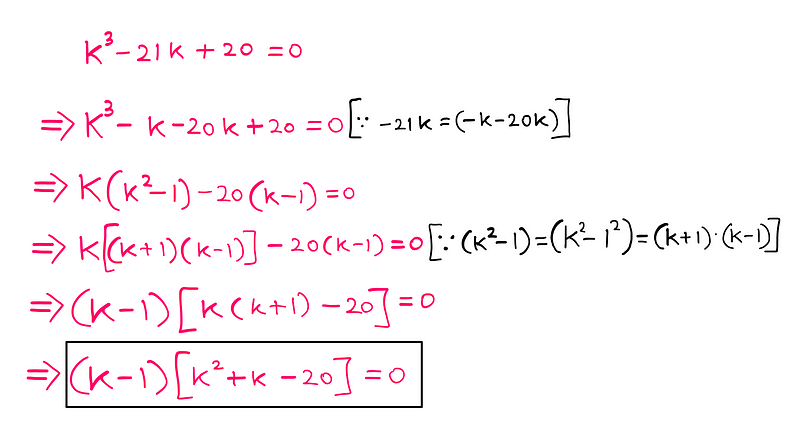
We can further refine this equation:

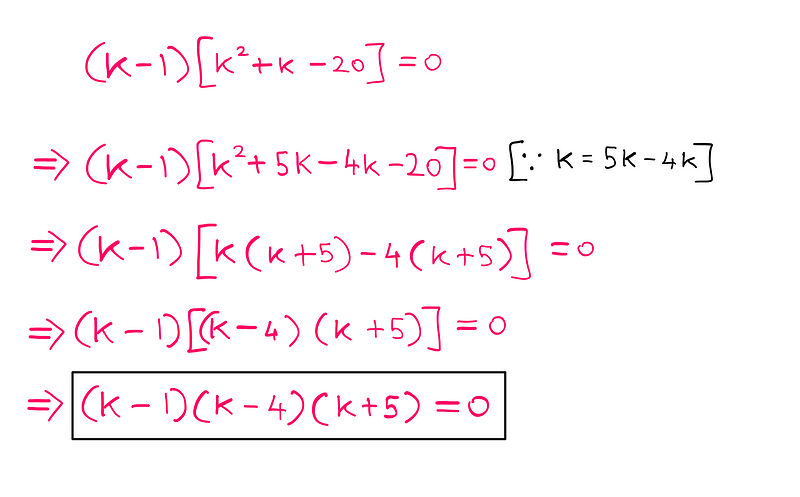
This leads us to three possible solutions for k:

1. k = x + y = 1
2. k = x + y = 4
3. k = x + y = -5

The Detailed Approach

In this method, we use the first equation (x² + y² = 7) and substitute the y values from our potential solutions. The resulting equations will lead us to quadratic forms.

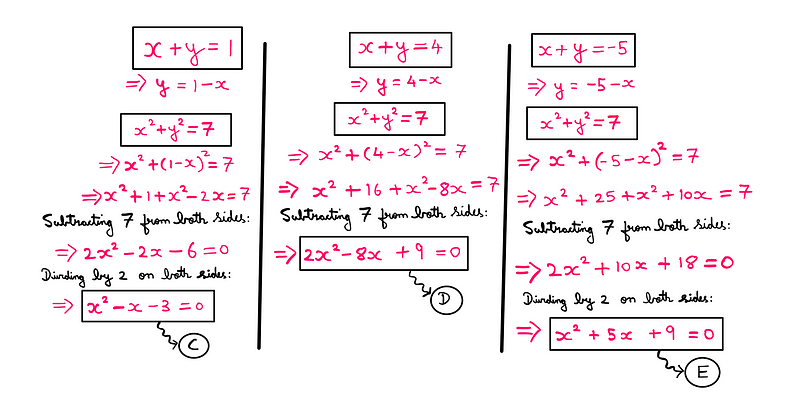
After evaluating these quadratic equations, we can check their discriminants.

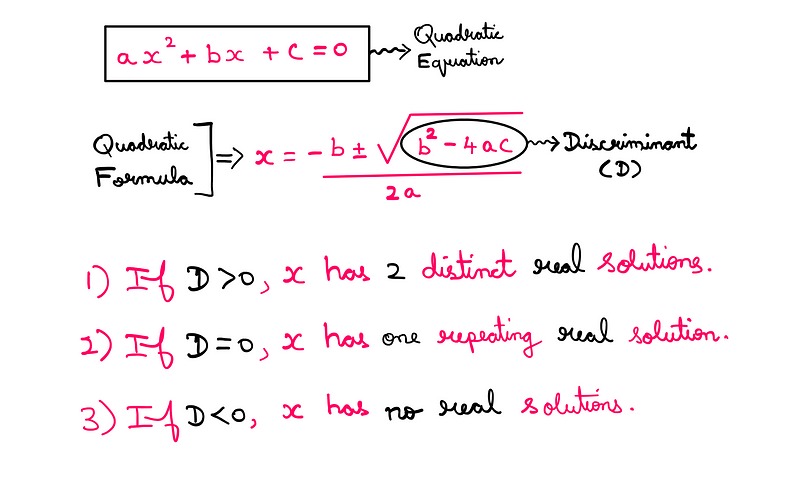
Ultimately, we find that only 'x + y = 1' is a valid solution.

The Quick Approach

Starting with our three k values:

1. k = x + y = 1
2. k = x + y = 4
3. k = x + y = -5

We can apply the Arithmetic Mean - Geometric Mean (AM-GM) Inequality to find valid solutions. The inequality states:

(x + y)² ≤ 2(x² + y²)

Calculating the right-hand side gives us:

2(x² + y²) = 2 * 7 = 14

Evaluating the left side for each k:

1. For k = 1: (1)² = 1 [< 14]
2. For k = 4: (4)² = 16 [> 14]
3. For k = -5: (-5)² = 25 [> 14]

This shows that only k = 1 satisfies the AM-GM inequality, confirming that the only solution is 'x + y = 1'.

If you've discovered an alternative method to tackle this problem, please share in the comments!